| ← Апрель 2012 → | ||||||
|
2
|
3
|
4
|
5
|
6
|
||
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
16
|
18
|
19
|
20
|
21
|
22
|
|
|
23
|
24
|
26
|
27
|
28
|
29
|
|
|
30
|
||||||
За последние 60 дней 16 выпусков (1-2 раза в неделю)
Сайт рассылки:
http://nanoworld.narod.ru
Открыта:
07-10-2005
Статистика
-2 за неделю
Доклад Александра Кушелева в Доме предпринимателей 2012-04-19
Выпуск 295 Лаборатория Наномир Когда реальность открывает тайны, Доклад Александра Кушелева в Доме предпринимателей 2012-04-19
Представьте себе, что у Вас в руках есть колба, наполненная эликсиром "вечной молодости". Вы уже проверили его действия на людях и его можно дать каждому, кто желает жить вечно и счастливо. Казалось бы, что в этот момент начинается эра счастья, но реальные события будут иными. Для начала торговли потребуется разрешение Минздрава. А его бесплатно не дают. Вы не сможете подарить людям вечную молодость, если у Вас нет денег, чтобы заплатить Минздраву. Парадокс заключается в том, что работники минздрава не смогут спасти от старости и смерти даже себя... Но на помощь, как обычно придёт теневая экономика. Эликсир "вечной молодости" будет продаваться подпольно, как наркотики, на которые Минздрав разрешения не давал... Приблизительно так будут развиваться события в современном несовершенном обществе. В лаборатории Наномир создан наукоёмкий продукт, который позволяет увидеть структуру практически любой молекулы белка приблизительно в 1000 раз точнее, чем это могут другие современные методы.
 Старые методы
 Новый метод  Старые методы
Новый метод
 Старые методы
Новый метод За каждую структуру белка в среднем заплачено ~10 000 евро. Сегодня определено около 80 000 структур. Мы можем ежедневно определять более 10 новых структур с точностью в ~1000 раз выше, чем это делают другие лаборатории. Но для начала продажи с ежедневным доходом 100 000 евро нам нужно опять-таки получение разрешения от международного Минздрава, который как всегда требует деньги вперёд... Как видим, современная цивилизация неспособна принять в дар новые научные открытия и технологии. Чтобы спасти цивилизацию от гибели, нужно сначала заплатить... И тут в цивилизованном обществе могут подключиться финансисты. Ведь билет на рынок высоких технологий не может купить только нищий изобретатель. Входной билет стоит около 100 000 евро, зато можно будет ежедневно продавать наукоёмкий продукт на сумму 100 000 евро. Покупка входного билет окупит себя в день начала продаж :) Что касается эликсира "вечной молодости", то он действительно почти готов. Анализ экспериментальных
данных убеждает в том, что существует один или несколько гормонов плаценты, которые отключают механизм старения во время беременности, чтобы защитить будущего ребёнка от преждевременного старения. Этот механизм подробно описан в рассылке "Новости лаборатории Наномир". В настоящее время завершается первый этап эксперимента и началась подготовка ко второму этапу, т.е. к выделению гормона "вечной молодости". Для этого этапа уже оплачены 200 клеток для лабораторных животных, которые 25 апреля
будут доставлены из Китая на Украину морским путём. Число лабораторных животных, необходимых для второго этапа, около 800. Это количество связано с достоверностью и необходимостью иметь достаточное количество животных на первом триместре беременности, т.к. именно в этот период плацента вырабатывает гипотетический гормон имморталин.  Результаты будут получены и без дополнительного финансирования, т.к. вечно-молодые мыши проявят
себя и без анализов. Но случится это не раньше чем через год, т.к. от старости мыши умирают в возрасте 2 лет, а если они проживут 3 года и при этом будут приносить здоровое потомство, это будет гарантией создания эликсира "вечной молодости". К сожалению, нашей планете каждую секунду от старости умирает несколько человек. За год от старости умрут десятки миллионов людей. Их всех можно было бы спасти, если создать эликсир "вечной молодости" на год раньше. У многих людей есть старые родственники,
которых можно спасти от старости и от смерти уже в этом году. Ведь достаточно начать принимать имморталин, и биологический возраст начнёт уменьшаться. Через год с любого возраста можно вернуться на уровень 30 лет.  На что тратятся деньги сегодня? Пока хватает только на корм для мышей. Мыши съедают приблизительно 300 рублей в день. 800 мышей будут съедать в несколько раз больше. А для определения, какой из ~100 гормонов плаценты
является гормоном "вечной молодости", нужны мембранные фильтры, ультрацентрифуга, препараты для анализов, зарплата дополнительного персонала и т.д. Желающие могут ознакомиться с программой эксперимента и сметой затрат: http://nanoworld.narod.ru/20110613.doc  Специалисты, которые проводят эксперимент, готовы ответить на Ваши вопросы. Мы поддерживаем связь по скайпу, поэтому ответы можно получить оперативно. Благодарю за внимание, какие будут вопросы? Создание средства для продления жизни Skype [17.04.2012
10:29:27] Геронтолог: Здравствуйте, Александр! В среднем, на поддержание стада стареющих животных и на питомник по размножению мышей необходимо 300 кг комбикорма в месяц. Минимальная цена в настоящий момент 530 грн за 100 кг. [17.04.2012 20:31:51] Кушелев Александр Юрьевич: Один инвестор решил передать Вам пока 3000 рублей в кошелёк вебмани. Код протекции 18475 Нужно получить в течение 24 часов, иначе обратно уйдут. [17.04.2012 22:39:19]
Кушелев Александр Юрьевич: Геном человека полностью прочтен. Можно ли найти в нём нуклеотидные кодирующие последовательности всех гормонов плаценты? [18.04.2012 11:38:15] Геронтолог: Здравствуйте. Александр! Деньги получены. Спасибо! По поводу генома - не все так просто. Прочтена последовательность нуклеотидов, но система регуляции активности генов до сих пор не изучена. [18.04.2012 11:43:23] Кушелев Александр Юрьевич: Да Бог с ней, с
системой регуляции. Сами гормоны плаценты известны или их в геноме не найти? [18.04.2012 11:43:48] Геронтолог: Гормонов плаценты очень много. Во многих случаях важно не само их количество, а соотношение между ними. К тому же часть этих гормонов может продуцироваться другими тканями. Так что придется еще тщательно разобраться в основных мишенях, на которые нужно будет воздействовать. [18.04.2012 11:44:46] Кушелев Александр Юрьевич: Должно
быть более простое решение [18.04.2012 11:46:09] Геронтолог: Биология наука неточная :). Но вы правы - решение должно быть простое, поскольку все гениальное просто. [18.04.2012 11:47:08] Кушелев Александр Юрьевич: Для начала нужно выяснить, возвращает ли
молодость сыворотка крови, взятая у мышей в первом триместре беременности? [18.04.2012 11:47:41] Кушелев Александр Юрьевич: Если да, то дальше нужно дробить её на фракции и искать минимальную фракцию, которая возвращает молодость. [18.04.2012 11:48:12] Геронтолог: Этим мы и займемся в ближайшее время! [18.04.2012 11:48:25] Кушелев Александр Юрьевич: Как я рад, что мы друг друга понимаем на этом
уровне. [18.04.2012 11:48:42] Кушелев Александр Юрьевич: Виктория Соколик убеждена, что смерть от старости - чисто случайный процесс :) [18.04.2012 11:50:02] Кушелев Александр Юрьевич: А я пытаюсь ей объяснить, что точка фатального возраста равносильна расстрелу: 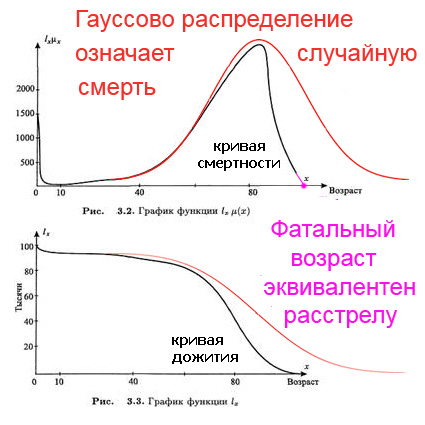 [18.04.2012 11:50:03] Геронтолог: Когда люди чисто случайно умирают в одном возрасте - это уже закономерность! [18.04.2012 11:50:15] Кушелев Александр Юрьевич: 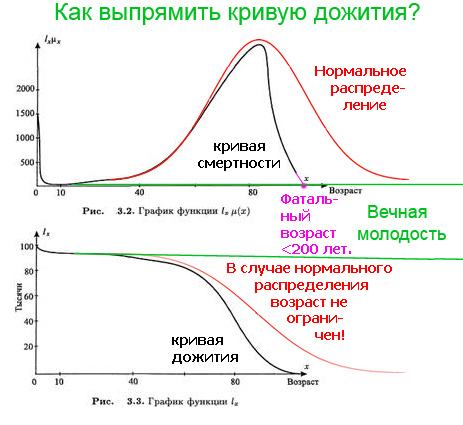 [18.04.2012 11:50:25] Кушелев Александр Юрьевич: Подробнее:http://nanoworld88.narod.ru/data/293.htm Victoria:
Доклад Александра Кушелева в Доме предпринимателей 19 апреля 2012 года (609 Mb, 27 минут): http://video.yandex.ru/users/kushelev2011/view/398/ Skype, 2012-04-18 [14:37:41] Кушелев Александр Юрьевич: Уважаемый Геронтолог! А Вам удалось испытать тест "толерантность к глюкозе"? [15:26:14] Кушелев Александр Юрьевич: Я-то это понимаю, но психология большинства инвесторов такова, что они хотят заплатить только за сорванный цветок, а всё остальное, благодаря чему этот цветок вырос их как бы не волнует [23.04.2012 20:01:48] Кушелев Александр Юрьевич: Добрый вечер! Александр Никонов: "Наука подбирается к тайне бессмертия" http://tv.km.ru/aleksandr-nikonov-nauka-podbirae Радиус электрона в корень квадратный из 3 меньше радиуса 8-электронной оболочки.
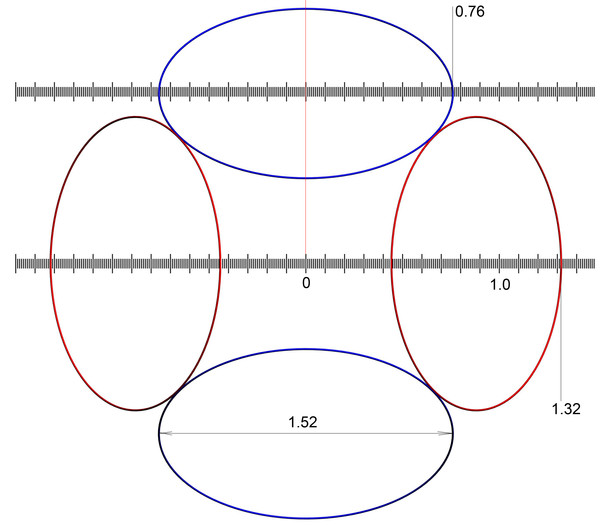
Кушелев: Диаметр 8-электронной оболочки кислорода по Голдшмидту 1.32 ангстрема (0.132 нм). В этом случае радиус электрона равен 0.76 ангстрема (0.076 нм). Я в программе Пикотех задал радиус электрона 0.5 * 1.7 = 0.85 ангстрема,
т.е. чуть больше, чем из рефрактометрии Голдшмидта. Так что "истина где-то рядом"
Protein is coded in genom and synthesized in ribosome as a structural template from peptide bound rotamers of sequence Victoria: Мой абстракт:
Кушелев: Что нам даст участие в этой конференции? Стоит ли овчинка выделки? Может быть за те же деньги можно издать научную статью в журнале BBA или Ribosome ? Victoria:
Кушелев: Так это и есть наш проект А сколько денег-то нужно? Victoria:
Кушелев: 700 долларов - это конечно мало по сравнению с первым проданным pdb-файлом за 10 000 евро. Поэтому инвесторы имеют серьёзный стимул оплатить научную рекламу пикотехнологии на англоязычной конференции. Будем надеяться, что нас поддержат. Кстати, а сколько стоит Ваша дорога туда и обратно? Патент школьного учителя из Германии 1951г. KARL SCHWAIGER, Atomic Structure PATENT SPECIFICATION 750.514 Date of Application and filing Complete Specification: Aug. 7, 1953. No. 2 1890/53. (Patent of Addition to No. 713,955 dated July 17, 1951). Complete Specification Published: June 20, 1956. Index at acceptance:-Class 146(2), G(4: 5E: 10). COMPLETE SPECIFICATION Improvements relating to Instructional Models for Representing Atomic Structure I, KARL SCHWAIGER, of 3, Selbacherstrasse, Gernsbach/Baden, Germany, a German citizen, do hereby declare the invention, for which I pray that a patent may be granted to me, and the method by which it is to be performed, to be particularly described in and by the following statement:- In the Specification of the Main Patent No. 713,955, an instructional model for representing atomic structure was described in which constructional elements were used of roughly cylindrical form, of a height approximately equal to half their diameter, particularly with a lemniscate-shaped cross-section, which for the purpose of illustrating atomic structure can be placed one against another and in layers one upon the other after the fashion of building blocks. It was also proposed therein to assemble the constructional elements, for the purpose of representing entire atoms or atom components, into polyhedral, and particularly octahedral, structures. The invention relates to a further development of this instructional model, wherein, for representing the atomic structure and different conditions of excitation, a proton is represented by two constructional elements placed side by side with oppositely directed positive and/or negative poles indicated thereon, and a neutron by two constructional elements placed one upon the other, self-contained and without indication of positive or negative poles, and the atoms or atom groups themselves, build up to form stereometric figures, are represented with the numbers of protons and neutrons corresponding to the atom or atom group to be represented. It is a particular advantage of the invention that, by different assembly of the individual constructional elements or groups of elements into atom models, carried out on the principle of the octahedron, the quality of the substances represented of belonging to particular atom series or atom groups of the periodic system can be explained and illustrated. By corresponding assembly it is then possible to produce therefrom, for example, crystallites and crystals, the properties of which can be determined in the form of models and coincide numerically with the results of research. On such octahedral structures the electron clouds surrounding the atom may also be represented, while the orbits of the electrons may be illustrated by bent wires or bands. At the same time. inward and outward radiations of heat and light waves can be marked on the model, for example by rectilinear and centrally directed wire clusters. Further features of the invention relate to the representation of atom systems, particularly molecules, by connecting together at their surfaces, edges or apices a plurality of polyhedra. For the purpose of representing certain properties of the substances, particularly elasticity, the various two-dimensional structures of the polyhedra or the polyhedra representing the atoms themselves can be elastically connected together, particularly in such manner that the polyhedra or polyhedral systems formed from them assume a stable shape under the action of a spring. With the aid of polyhedra connected together in this manner it is also possible to show by the elastic turning over of individual polyhedra how the properties of the substances vary, for example by deformation under tensional or compressive forces, on magnetisation or the like, a surface bond between the polyhedra being for example produced from an apex or edge bond. The modulus of elasticity or the elastic limit, the electrical and thermal conductivity, and the like, can thus be represented in a clear manner and calculated arithmetically from the various polyhedron dimensions. In addition, the invention refers to the representation of the thermal oscillations on such atom models, since by the representation of the three stable axes of revolution of the octahedron and of the appertaining possibilities of oscillation the production of the atom spectra can be shown qualitatively and quantitatively. -- - With the aid of the following examples of the instructional model forming the subject of the present invention, the latter, its application and the resulting possibilities of representing the results of scientific investigations and their elaboration will be explained in greater detail. In the accompanying drawings:- Figures 1 to 9 show the representation of a -series of atom systems of the simplest structure in various conditions of excitation. Figures 10 to 12 the special nature of the atomic structure in the case of rare gases. Figure 13 shows an octahedral atom with a representation of the orbits of the electrons and the heat and light radiations. Figure 14 shows the same system as in Figure 13, omitting the inner electron orbits. Figures 15 to 18 show a representation of the three possible types of bond of three dimensional atomic systems. Figure 19 shows the representation by way of example of a molecule composed of atom models (benzene). Figures 20 to 22 show an example of a paramagnetic metal bond. Figures 23 to 25 show stereometric and crystallographic representations of this bond. Figures 26 to 30 show similar representations of a diamagnetic metal bond. Figures 31 to 33 show a representation of the possible oscillations of an octahedral atom in vector representation, and Figures 34 to 40 show a representation for the production by means of a model of atom spectra on rotation of the octahedral atom about the three possible stable axes of rotation. In the Specification of the main Patent No. 713,955, the representation of the structural component of the atoms in the form of vortex rings, on the analogy with hydrodynamic vortex rings, is explained. The vortex rings may be considered to consist of a certain number of revolving m0 particles (neutral particles of the order of magnitude of 10" cm.) moving in circular paths. A vortex ring of this type, corresponding to the direction of rotation of the rn0 particles rotating in the vortex ring surface, acts towards one side as a positive pole (or hydrodynamic "source ") and towards the other side as a negative pole (or hydrodynamic "drain "). In accordance with known hydrodynamic principles, such vortex rings attract one another or repel one another, depending on whether their positive or negative poles lie opposite one another. They can be so assembled that, for example, the positive pole of one points upward and that of the other downwards, thus forming a proton in accordance with Figure 1. If two vortex rings are pressed on∙ one another with their negative poles in such manner that although both "sources" are exhausted, yet the vortex rings are fully maintained, there is produced in accordance with the theory underlying the Application a neutron, which is for example 7 illustrated in Figure 2. In addition, Figure 3 shows a hydrogen (H) atom formed from four vortex rings, Figure 4 a nascent hydrogen atom, Figure 5 a hydrogen molecule formed of eight structural components (H,), already built up in accordance with an octahedral system, Figure 6 is a '-particle made from. eight components (doubly ionised helium atom), Figure 7 a helium isotope of 12 components, Figure 8 a helium atom made of sixteen components and arranged in the shape of an octahedron, and Figure 9 a carbon atom composed of 48 components. Figure 10 shows a helium atom as shown in Figure 8, in cubic representation; In similar manner all other atoms (including their isotopes) can also be represented, while the breakdown of the triangle structure of the octahedron surface into quadrilaterals, pentagons, and hexagons and the' :chemical valency associated therewith above all, play- I an important part. The representation by models, in addition to other properties, also for example allows it to be seen why atoms of particular mass numbers, for example atomic weight A,=5 I mass units (ME) and A9 =8 ME, do not occur in nature. The corresponding atoms can be assembled in the form of models only in the form of unstable structures; a stable geometrical structure is impossible. The He atom represented in Figure 8 exhibits an octahedron shape in the (111) direction (using the usual crystallographic notation). If it is observed from the (011) or (110) direction, a cube shape can be seen (Figure 1). By stratifying such He atoms to form larger cubes, the inert gases with higher atomic weights can be represented, for example krypton (Figures 11 and 12), Figure 12 showing the construction of a Kr model composed of the structural components. The cube form in conjunction with the porous structure makes both the chemical. neutrality and also the hitherto unexplained: electron-permeability in certain directions immediately plausible. In similar manner the atom structure enables for example the low cleavage tendency of Uranium 238 or the high cleavage 'tendency of Uranium 235 to be explained. The same is true of mechanical strength (elaideity and plasticity), conductivity (thermal arid electric), thermal expansion, melting points, and so on. The construction and decomposition of atoms can be represented particularly clearly if the individual constructional elements consist of permanent magnets having an axial field; or the models of the atoms or atom components can be used as finished octahedral structures. If desired, in the use for model purposes of triangles, polyhedra or the like, it is also possible to abstain entirely from the particular representation of the individual structural components. In consequence of the heteropolar arrangement of the triangles in the octahedron, hydrodynamic potential clouds or electron clouds are produced in accordance with Figure 13. The emission of the electrons is effected through the hydrodynamic "source" energy. They are re-absorbed in the hydrodynamic "drains." The resulting orbits of the electrons are represented in Figure 13 as approximately circular paths p in the form of bands inside an enclosing spherical surface t. The enclosing spherical surface consists in the model, for example, of transparent material or a wire net and represents physically the surface enveloping radiations of heat and light waves issuing from the atom. Apart from the hydrodynamic (electrodynamic) potential clouds indicated by these paths, thermal longitudinal waves also occur in the arrow directions marked (c) and (C). In Figure 14 the same structure as in Figure 13 is represented, while however the potential loops lying inside the sphere boundaries are omitted. The inflowing longitudinal waves are here indicated by the axes g,, g,, g,, g4. The different structure of the atoms results in the multiformity of the mutual attraction forces, which in turn results in coordination constraint to form molecules and crystals. As is clear from the atom model of the octahedron type, the binding of the atoms to one another can take place at the point s (Figure 15), the edges k (Figure 16) or the surfaces f (Figures 17 and 18), Figures 17 and 18 showing the two possibilities of the atom position in the case* of the surface bond. Depending on the type of bond, different physical properties are produced. For example, impulses of a mechanical, thermal and also electrical type are transmitted with an intensity which is dependent on the type of bond as shown in Figures 15 to 18. As an example of a molecular structure with simultaneous surface and edge bonds, Figure 19 shows the fine structure of a benzene ring which shows two atom groups C3H3 in which the carbons C have a surface bond at f, while the two half-rings have in each case only a half edge bond with one another at k in the plane of symmetry m-m for geometrical reasons, in accordance with the angles a and (3. All chemical and physical properties of the benzene ring can be explained thereby. Hinged or resilient connections of the atoms' in the crystal or atomic systems and the behaviour, of the substances under the action of mechanical, thermal or electrical forces can be demonstrated. For example, an atom chain 0, 0,, 0, arranged in a row with edge bonds (Figure 16) for the atoms can be converted by alternate hinging over of the neighbouring atoms over one edge k in each case into a surface-bonded atom chain 0, 0,, 0,, corresponding to Figure 17 or 18, and vice versa. The bonds of individual atoms to one another or else of the atom constituents (ions) to one another can be illustrated in the model for example by springs or elastic bands or magnets representing the binding forces. However, the model can also be made of material which is in itself resilient (possibly only at the bond points), for example rubber or the like. Figure 20 shows a model for a combined apex and surface binding of metal atoms r, to r6. The arrangement of the metal atoms takes place according to the octahedral system illustrated in Figure 23. The atoms have here partly surface bonds, while in other cases only apex bonds are provided, while- for stereometrical reasons an angle of S = 19 30' remains between the surfaces of neighbouring atoms. Under the action of compressive forces, the crystal nucleus (6 atoms) shown in Figure 20 passes through the intermediate state shown in Figure 21 into the state shown in Figure 22. In Figures 21 and 22. for the sake of clarity, only the front three atoms are illustrated. The transition takes place owing - to the fact that the atoms and in this potential condition lie with their neighbouring faces on one another, reducing the angle 8 = 190 30' to 7=0. These Figures show a model which is made, for example, of cardboard, sheet metal, or the like, while the edges of the atom can be connected together elastically by rubber bands or the like, which are not shown in the drawing. Stereometrically this may be expressed by the fact that, while retaining the grid type (Figure 23), the triakis octahedron (Figure 20) (crystallographically in Figure 24) passes over into a rhombic ∙ dodecahedron as shown in Figure 22 (crystallographically in Figure 25). The axes x, y, z in Figure 20 are likewise indicated in the representation shown in Figure 24. When the pressure is relaxed, the atom passes back into the state shown in Figure 20 from the state shown in Figure 22, which can also be distinctly illustrated in-the model by the elastic construction of the individual atoms. The atom structure shown in Figure 20 corresponds to a paramagnetic metal bond, in which the metal on account of the gaps has low thermal and electrical conductivity but is nevertheless distinguished by high elasticity (movability of the atoms by 19 30'). Figures 26 to 30 show in contradistinction thereto a diamagnetic metal bond which has high thermal and electrical conductivity but on the other hand low elasticity. The structure of such an atom group constitutes a kind of hexahedron which is composed of nine neutral atoms p to p. which are illustrated diagrammatically in Figure 28 and in perspective in Figure 26, these atoms being bound by a pure surface bond to a central atom. If 6 further atoms are brought into the six hexahedron troughs, they must then be deformed under the action of external pressure forces similarly to Figure 27 and all fifteen atoms (Figure 30) then form the structure of a tetrakis hexahedron (Figure 29) which is well-known in crystallography. A comparison with the atom group shown in Figures 20 to 25 shows plainly the structural difference. With the crystal nucleus of the surface bond type (Figures 26 to 30) free movability no longer exists for the individual atoms. On the other hand, a metal bond of this type permits mutual displacement of the various atoms while retaining the surface bond, the atom surfaces sliding over one another, which explains the high plasticity of such metals. The movement of the atoms when a substance is in the gaseous phase can also be represented with the models shown in Figures 31 to 40. Figures 31 to 33 show the possible oscillations of an octahedron atom, namely with reference to the three planes (001), (010) and (100), which are determined by the stereometrical conditions of the octahedron. The oscillation directions are here indicated by arrows. The models can be so constructed in accordance with these possible oscillations that in the case of Figure 3.1 two pyramids can be moved synchronously in an apex oscillation in relation to one another perpendicularly to the (001) plane, in the case of Figure 32 four sphenoids can be moved in an edge oscillation synchronously in relation to one another perpendicularly to the, (101) plane and in the case of Figure 33 eight triangles can be moved in an edge oscillation synchronously in relation to one another perpendicularly to the (111) plane. By Figures 34 to 40 it is intended to show what stable rotational axes exist for the octahedron atom. Figure 35 is a ground plan corresponding to Figure 34, Figure 40 a ground plan corresponding to Figure 39, while Figures 36,'37 and 38 show three different states of movement for the same atom during rotation about the same axis. Figure 34 shows a model with F-axis (axis of rotation running through the centres of gravity of two surfaces lying opposite one another), Figure 36 a model with S-axis (axis of rotation running through two apices lying opposite one another) and Figure 39 a model with K-axis (axis of rotation running through the centres of two edges lying opposite one another). The states of oscillation shown in Figures 31 to 33 arc caused by intra-atomic charges, such as are produced by thermal and electrical irradiation, for example in the gaseous phase. As soon as the internal atomic pressure exceeds the normal atmospheric pressure of the ether bearing on the atom surface, the atom surfaces are lifted up until the internal excess pressure can escape to the outside. These amplitudes of the oscillating surface are diagrammatically indicated by a in Figures 34, 36 and 39. Surface oscillations as shown in Figure 33 are produced by rotation, about the surface axis of Figures 34, 35. Apex oscillations as shown in Figure 31 are caused by rotations about the edge axis of Figures 39 and 40, and edge oscillations as shown in Figure 32 by rotations about the apex axes of Figure 36. In the case of the latter, two types of oscillation may occur: 1). Predominance of internal pressure over centrifugal force at a low speed of rotation gives a parallel oscillation with an amplitude a as shown in Figure 36. 2). Predominance of centrifugal force over internal pressure at a high speed of rotation gives an angular oscillation octahedral deformation b or b' as shown in Figure 37 and Figure 38, respectively. The models can for this purpose once again be made elastic, the edges of the neighbouring surfaces being for example joined together by elastic bands in such manner that on rotation about the f, s or k axes under the action of centrifugal force, gaps are produced between these edges. By stereoscopic connection of rotation and oscillation the atomic or molecular spectra of the gaseous substances are then produced with mechanical constraint. If we designate by r the speed of rotation of the whole atom and by s the frequency of oscillation of the atom surfaces, we can at once write the Balmer formula of the spectral lines as follows: (formula here not possible in Microsoft Word) The main series (HS) in the light spectrum then corresponds to a rotation of the atoms about the surface axis (Figures 34 and .35), combined with a surface oscillation (Figure 33). The subsidiary series are produced by combination of rotation and edge oscillation, as shown in Figure 32. Such oscillations, however, can be formed only by rotation of the atoms about their apex axis, namely, at a low speed of rotation as such with Wand amplitude "A" as shown in Figure 6and in the case of a greater rotational impulse as b deformations as shown in Figures 37 and 38. Parallel oscillations produce the sharp lines of the ILNS (second subsidiary series), while the' angular oscillations cause great rotational speed oscillations and thus lead to unsharp spectral lines of the 1st subsidiary series. The Bergmann series (BS) observable only with a high rotational impulse is produced by combination of an apex oscillation (Figure 31) with the edge rotation (Figure 39) which can occur in the case of an octahedron atom for mechanical reasons only at maximum excitation. For the representation of the spectra by models, according to the present invention the "positive" atom surfaces can be provided with small reflecting discs, which arc intended to mark the natural frequency of the atom surfaces on rotation of the atom models. With the aid of such atom models it is therefore possible to represent with full clarity the atomic processes which lead to the formation of spectral lines of any kinds, which hitherto with the aid of "mechanistic" atom models it was hitherto not possible to do. What I claim is:- 1. Instructional model for representing atomic structure by the use of constructional elements of roughly cylindrical form, of a height approximately equal to half their diameter, which can be placed one against another or one upon another after the fashion of building blocks and assembled to form three-dimensional and particularly octahedral structures, in accordance with Patent Specification No. 713,955, wherein, for representing the atomic structure and different conditions of excitation, a proton is represented by two constructional elements placed side by side with oppositely directed positive and/or negative poles indicated thereon, and a neutron by two constructional elements placed one upon the other, self-contained and without indication of positive or negative poles, and the atoms or atom groups themselves, built up to form stereometric figures, are represented with the numbers of protons and neutrons corresponding to the atom or atom group to be represented. 2. Instructional model according to claim 1, wherein, for the representation of particular atom properties or effects, the three-dimensional structures representing the atoms are provided with extra representational elements such as bands axes of rotation, arrows, envelopes, or the like, or are constructed to be variable, for example elastic. 3. Instructional model as claimed in claim 2, wherein for the representation of electron orbits, loop-shaped bands, wires, or the like are provided, passing out of a surface of the polyhedron and returning to the neighbouring surface, or for the representation, of inward and outward radiations of heat and light waves, radial bands, wire bundles, or the like are provided, while the mutually alternating positive surfaces and negative surfaces of the polyhedron may be correspondingly characterised. 4. Instructional model as claimed in claim 3, wherein, while the representation of the individual orbits or radiations may, if desired, be omitted, the polyhedron is surrounded by a spherical surface enclosing the orbits and made for example of transparent material or else in the form of a wire net. 5. Instructional model as claimed in any one of the preceding claims, wherein for the representation of atoms systems composed of atoms, particularly molecules, a plurality of polyhedra are connected together at their surfaces, their edges, or their apices. 6. Instructional model as claimed in any one of the preceding claims, wherein for the representation of the possible oscillations of the atoms the various surface structures of the polyhedra, or for the representation of the elasticity of the materials, the polyhedra themselves which represent the atoms are connected together elastically, particularly in such manner that the polyhedra or polyhedron systems formed from them assume a stable shape under spring action. 7. Instructional model as claimed in claim 5 or 6, wherein the connection of the individual models of the atom components of the atoms to one another is effected by means of cords, particularly elastic cords, such as rubber bands or the like, which join together elastically the surface structures which abut at an angle. 8. Instructional model as claimed in claim 5 or 6, wherein the connection is produced by magnetic action, the edges of the surface structures or polyhedra being for example constructed as magnets. 9. Instructional model as claimed in any one of the preceding claims, wherein the polyhedra are connected together to form regular three-dimensional structures of a higher order by edge or apex bonds, in such manner that between the individual surfaces or edges of neighbouring polyhedra free angular spaces (in the case of octahedra particularly with angles of 90 30') are produced and by hinging over (particularly elastically) individual polyhedra the apex bond can be converted into a surface bond and/or the surface bond into an edge bond. 10. Instructional model as claimed in any one of the preceding claims, wherein the polyhedra are connected together into regular three-dimensional structures of a high order with edge or apex bonds, in such manner that between the individual surfaces or edges of neighbouring polyhedra free angular spaces (in the case of octahedra in particular, with angles of 190 30') are produced, the surface structures of the polyhedra are connected together at individual edges only at points or elastically, so that under radial pressures at the edges, a gap. can be produced between said edges, and the apex or edge connection of the polyhedra to one another can be converted into surface abutment (surface bond) by reducing or eliminating the angular spaces. 11. Instructional model as claimed in any one of the preceding claims, wherein for the representation of the intra-atomic oscillations, the polyhedra are furnished with zero planes running through the edges of the polyhedra or with vectors to indicate the directions of the oscillations in the case of apex, edge, and surface oscillations, while the surfaces, edges or apices can be elastically fastened. 12. Instructional model as claimed in any one of the preceding claims, wherein, for the representation of the spectrum generation M the gaseous state of the substance whose structure is represented by the model, the polyhedra are furnished with axes to characterize the stable possibilities of rotation, while the axes may run through the apices, through the centres of edges, or through the centres of gravity of surfaces of the-polyhedron. 13. Instructional model as claimed in claim 12, wherein the surfaces of the polyhedra are resiliently connected together, so that under the action of ccntruga1 forces or other external forces they yield in relation to the axis of rotation or in relation to one another cc can be caused to oscillate, while the arrangement may be such that the surfaces in each case perform a movement of translation or an angular movement about one at their edges. 14. Instructional model as claimed in claim 12 or 13, wherein the "positive" surfaces of the polyhedra are provided with small reflecting discs which on rotation in accordance with claim 12 and 13 can mark the natural frequency of the surface oscillation. 15. An instructional model for the representation of atomic structure, different states of excitation and/or particular atom properties or effects, substantially as hereinbefore described with reference to the accompanying drawings. JENSEN & SON, 77, Chancery Lane, London, W.C.2, Chartered Patent Agents. Leamington Spa: Printed for Her Majesty's Stationery Office, by the Courier Pies.-1956. Published at The Patent Office, 26, Southampton Buildings, London, W.C.2, from which copies may be obtained. Кеннету Снельсону 85! Ответ на письмо Кеннета Снельсона Kenneth Snelson: Can either of you tell me how Mr. Ogzhevalskovo explained his model? Кеннет Снельсон: Можете ли Вы рассказать мне, как мистер Огжевальский получил свою модель? Kushelev: We have this article only: http://www.nanoworld.narod.ru/index.htm Кушелев: У нас есть только его статья...
Wave tube model. My model same. Волноводная модель. Моя модель такая же. Kenneth Snelson: Why are his electrons represented as rings? Кеннет Снельсон: Почему его электроны представлены кольцами?
Kushelev: Ogrzevalski picked up a form of wave guides. Кушелев: Огжевальский взял форму волноводов. Kenneth
Snelson: Does Mr. Ogzhevalscovo mention Louis de Broglie's 1924 "matter wave" model in his paper?
Огжевальский: Обратим внимание на подобие и различие между классическим уравнением Даламбера и релятивистским квантовым уравнением волн де Бройля Autotranslation: let's pay attention to similarity and distinction between Kenneth Snelson: How does his atom's electrons work? Kushelev: To similarly closed wave guides All our works are a pikotechnological basis. Mew Article / Новая статья: http://nanoworld88.narod.ru/articles/pi … _01_24.doc Details / Подробности: http://nanoworld88.narod.ru/data/291.htm We participate in the international competition CASP10:
Details / Подробности: http://nanoworld88.narod.ru/data/285.htm New standard / Новый стандарт: http://nanoworld88.narod.ru/data/287.htm Science for business / Наука для бизнеса: http://nanoworld.org.ru/topic/283/ Eternal youth - the main subject / Вечная молодость - главная тема Warmest wishes / теплые пожелания, Патент Кеннета Снельсона (1964г.) Kenneth Snelson: Dear Sasha, Thank you for the explaining how Ogzhevalskovo described his model. I don't know how different a wave-guide is from Louis de Broglie's "standing wave". As you know, Sasha, my atom does not presume to be a work of science, but rather it is an artist's picture created from speculative reasoning based on the 1924 model of Louis de Broglie. In the Snelson atom model, the electron particle is drawn into the nuclear electrical sphere and immediately is transformed into a (circular) de Broglie standing wave -- caterpillar to butterfly. It is a device, an "atom within the atom" that has an orbital and a spin magnetism and a stabilizing angular momentum and an electrical charge. Its quantized wavelength and velocity are dictated in the atom by the nuclear electrical sphere's intensity. The matter-wave's wavelength and velocity are "keyed" in the electrical sphere analogous to an aircraft guidance system. In my model the electrons' de Broglie standing waves can reside equatorially or on small circle domains, requiring only the proper wavelength for any particular energy sphere. De Broglie waves are impenetrable to one-another. Pauli's exclusion principle's physical explanation is that matter waves in an atom cannot occupy
the same space at the same time. Question: Are the Kushelev atom or the Ogzhevalskovo atom very different from the Snelson atom? Again, best wishes, Ken United States Patent Office 3,276,148 The present invention relates to a three dimensional model useful as an educational or research device for structurally representing atomic forms and more porticularly to a model which demonstrates structural reasons for the different types of electronic orbitals and shows why only certain numbers of electrons are present at a given energy level. In addition, the model of the present invention defines for the first time a principle of structure involving the electrons’ orbital magnetic fields. In the past, various theories have been adanvced to explain the electronic structure of the atom. Structural models of the atom incorporating these theories have, however, left unexplained certain aspects of the quantum theory. The Rutherford-Bohr model of the hydrogen atom which came into being in 1913, represented the atom as a miniature planetary system and although this model was reasonable mechanically, it presented other difficulties. According to classical electromagnetic theory, charged particles accelerated by electrical fields are expected to radiate electromagnetic energy. Because of this, an atom with a planetary electron experiencing angular acceleration around the nucleus should collapse in a fraction of a second by loss of energy. Niels Bohr, therefore, hypothesized that there must be stabilized states at which the electron could rotate about the nucleus and not lose energy. His model of the hydrogen atom represented these "stationary states" or energy levels as concentric circular orbits at which the system was stable. Energy was then given off or absorbed only when the electron jumped from one energy level to another. This model of the atom as advanced by Bohr was, however, shown to be inadequate in certain respects. Arnold Sommerfeld, a German physicist, noted that Bohr's model could not account for the subtleties in the hydrogen spectra. Sommerfeld considered that Bohr's circular orbits might be supplemented with a system of elliptical orbits in the model to account for these additional lines. The prescribed ellipses had the same major axis as the Bohr form, but narrower minor axes. Since the data which Sommerfeld applied to his model of the atom was known spectroscopic data, the spectral names were attached to the various orbital types. Thus, the letters s as used for sharp lines, p as used for principal lines, d as used for diffused lines, and f as used for fundamental lines were employed to designate the electrons of the various new elliptical orbits. In this modified model of the atom, the first energy level or shell required only the circular orbit or s electrons while the second shell had two types of orbits, one circular and one elliptical with the electrons of the two orbits designated as s and p electrons, respectively. The third shell required three types, s, p. and d; and the fourth shell required four s, p, d, and f. In a later development, Louis de Broglie postulated that matter, like electromagnetic energy might also have an associated wave aspect in addition to its particle-like qualities. This speculation was proved to be correct where experiments showed that electrons could be diffracted by crystals much in the manner of light waves. To Bohr's atom was joined the de Broglie wave hypothesis, which explained the stationary states as standing wave periodicities. The resulting theory postulates that the electron can settle at only those distances from the nuclear charge where it can fit whole numbers of complete wavelengths. The circumference of the electron's smallest orbit is equal to exactly one complete wavelength. The second orbit has that circumference which can accommodate two complete wavelengths, the third three, and so on. The reason for this is that the matter-wave of the electron is a standing wave. It is continuous throughout the cycle of orbital motion and must therefore be in phase with itself, restating its own pattern at each cycle. Without the proper circumference to permit this, it would interfere destructively with itself. In a successive development Erwin Schrodinger evolved his wave equation based on the earlier work of Bohr, Sommerfeld and De Brogue. Wave mechanics, which resulted from Schrodinger's wrok, defines electron interactions statistically. Its difficulties lie in the many numbers of possible interactions in any atomic system involving several electrons. For this reason the hydrogen atom, with a single electron, still serves as the prototype for all atoms and wave mechanics is founded on the assumption that electron waves surround the nucleus much in the manner of a single electron of hydrogen. When an atom has large numbers of electrons, their interactions can only be dealt with as probabilities. Modifying this picture is Werner Heisenberg's "uncertainty principle," which describes the limit to which it is possible to be certain where a moving electron can be located. It is proper only to speak of "charge clouds" which describe the probability of finding an electron in a given volume of atomic space. It is important to note that models which evolved in several stages attained their features additively over a period of time. The most arbitrary additions in terms of experimental evidence were Sommerfeld's elliptical orbits. They were introduced originally to account for energy differences of the various orbits in the same shell in terms of the relativistic mass change which the electron might experience if it were to accelerate and decelerate around the nucleus in an elliptical manner as does the planet Mercury around the Sun. The elliptical electron orbits failed mathematically to account for these variations in energy. For this reason the original purpose was never fulfilled. The ellipses were also meant to account for the change in angular momentum of s, p, d and f orbitals by the assumption that the rounder an orbit, the greater was its angular momentum. This required, however, that a electrons have orbits with zero minor axes because they have no observable angular momentum. Because they would therefore move only transversely, they would be required to pass through the nucleus, which was clearly not possible. In addition, any elliptical orbit would be required to precess in a perihelion fashion as does, for example, the planet Mercury and therefore would have no stable orientation by which one might observe its angular momentum. So ellipses failed in this respect as well. In the later forms which elliptical orbits assumed, according to the charge cloud modifications of Schrodinger and Heiscnberg, precise orbits were no longer referred to, but the elliptical form was retained as a means of differentiating between orbital types in the same shell. The elliptical orbits also served to provide the electrons' orbits a direction in space relative to the nucleus, thereby making it possible to represent bonding angles in molecular models. The present invention accomplishes this required 'directionality more effectively and more logically than the previous model. This will be demonstrated below. Another serious disadvantage of the conventional model is its inability to indicate how the electron moves in order to occupy a charge cloud. Electron motion is nevertheless real and is inevitably discussed in association with orbital angular momentum and orbital magnetic fields. It is also discussed in regard to the orientation of the electron's spin relative to its orbital motion. The new model provides the required frame of reference to define these relationships. So far only the individual electron and its various possible orbits as represented by previous models has been discussed. The inadequacies and contradictions presented by these models are further demonstrated when models representing complex atoms are considered with reference to Paull's "exclusion principle" which provides a classification system by which all electrons in a single complex atom can be differentiated. The "exclusion principle" assigns each atomic electron four "quantum numbers" in order to describe an energy state. These four factors are: (1) the principal quantum number n which describes the shell number and which can have values of 1, 2, 3, 4 . . . as in Bohr's original planetary model; (2) the azimuthal quantum number l which describes the orbital eccentricity like Sommerfeld's ellipses as well as the value of the orbit's angular momentum and which can have values of 0, 1, 2, 3 (n-l) corresponding to s, p. d and f electrons; (3) the magnetic quantum number which describes the direction in which the plane of the orbit faces and which can have values of -1, -1+1 ... 0 .. . -1, and (4) the spin quantum number ms which describes the direction in which the particle electron spins relative to its motion in orbit and which can have values of ±1/2, that is, spin can be in the same or in the opposite direction as the electron's orbit. No two electrons in the same atom can have identical sets of quantum numbers according to the "exclusion principle." Electrons are shown, therefore, to exclude one another from the energy position which each occupies and are, in this way, similar to larger aggregates of matter which cannot occupy the same space at the same time. Beginning with hydrogen's single electron, the numbers permitted at consecutive energy levels according to the "exclusion principle" can be reviewed. Helium follows hydrogen in the table of elements with a second nuclear charge and a second electron which also resides in the first level. The fact that helium is chemically inert indicates that its two electrons complete the first shell. This tightly bound system is due to a phenomenon known as "spin pairing." Electrons, as well as many elementary particles, possess an intrinsic top-like quality whether they are at rest or in motion. Spin provides the particle with a fixed quantity of angular momentum and a small magnetic field. As an electron moves in orbit it can spin in the same direction as its rotation in orbit or in the reverse direction. Helium electrons or any such spherical s pair have opposed spins and they are pictured as following one another about at opposite sides of the nucleus because of the repelling force of their like electrical charges. They can be thought of as two points on a wheel, which can precess freely as the wheel rotates, describing a spherical volume of space. Because they are always opposite to one another, as if fixed in space, their magnetic spin fields are fixed in relation to one another. In order to reach their minimum energy state, the two spin fields assume a magnetically attractive antiparallel association which helps overcome their repelling electrical energies. Until spin was discovered and incorporated into the "exclusion principle" it was thought that s electrons were simply two point-charges which moved along the same orbit. But now, s electrons, because their antiparallel spin fields were shown to alter each other's courses slightly, are regarded as occupying separate orbits. Looking at the second completed shell of the atom where there are a total of eight electrons, two subshells are shown. One of the subshells designated as the 2s subshell includes two s electrons which form a spherical configuration as in the first shell while the remaining six electrons occupy p orbitals and form the 2p subshell. These p orbitals in the conventional models are not spherically symmetrical charge-clouds, but reflect the elliptical p orbital form described by Sommerfeld and as a configuration they are shown as penetrating the inner shells and extending outward from the nucleus along x, y, z axes of the atom. Due to this, these models have been questioned because they give no explanation as to how the p electrons can move in and out through the first and second shell s electron spheres without interfering with the stability of the system. This problem becomes more complex with conventional models representing the third and fourth shells of an atom. In the third shell another spherical s subshell is formed plus another subshell of six p electrons with their penetrating charge-clouds. Added to this, however, is a third subsheil of ten electrons which also penetrates the inner shells. This is the d subshell or d orbitals. And in the fourth shell, all of the configurations of the third shell are repeated, but this shell further includes another subshell with fourteen penetrating electrons occupying f orbitals. In any effort to define a workable system or model showing electron trajectories or wave-paths for a many electron atom, we are therefore confronted with a dilemma in topology as to how a plurality of matter-waves can occupy stationary states and still avoid destructive interference; or in terms of particles, how large numbers of electrons moving about the nucleus can avoid random perturbations. The problem with present atomic models is a mechanical one, for electrons or any charged particles attract or repel one another by producing and exchanging packets of energy, one to the other. If, however, this were to actually happen at random between electrons of different energies as indicated by present atomic models, the entire conception of stable energy levels would be inexplicable and spectroscopy would not show the sharp and limited lines which are the fingerprints of the different kinds of atoms. The difficulty is further intensified in the heavier atoms because, with the increase of nuclear charge, the kinetic energies of the inner electrons become very great, and there is no way to explain how the outer electrons, with comparatively small kinetic energies, can repeatedly penetrate the inner shells without actually being removed from the atom by internal collisions. According to the teachings of the present invention, a new model of the atom can be constructed to fill the requirements of the quantum theory by giving a structural and spatial meaning to all four quantum numbers needed for describing the energy state of each electron. Also, the new model of the present invention presents a logical solution to the interference problem of interpenetrating charge-clouds by providing the orbit of each electron with its own domain of spatial occupancy. In addition, the individual orbits of each subshell as represented in the new model spatially define the magnetic fields which result from the orbital motion of the electron and from the inherent spin of the particle electron and in this way present a structural explanation of the in and s quantum numbers. Generally, in building the atomic model according to the teachings of the present invention, the first shell will represent two s electrons have one-wave cycles surrounding the nucleus of the atom in an equatorial way. For the second shell of the atom, however, the electron's two-wave cycle is shown as having an alternate orbital form or p orbital which contains just one wave with the circumference of this one-wave orbit having half the circumference of the two-wave orbit or s orbital form. Following this procedure for the remaining shells of the atom, the new model represents all the orbits as standing waves but only with s orbitals surrounding the nucleus in an equatorial way. In the new model, the second, third and fourth shells of the atom are broken down into subshclls for separately containing the different types of possible orbitals s, p. d, and f. And in the p, d, and f, subshells, the electrons are shown as circling in a plurality of individual orbits offset from the nucleus of the atom with the total number of orbits in each completed subshell, in turn, defining that subshell. Referring to the drawings: FIG. 1 is a partial diagrammatic view of the first and second shells of an atom as represented by the model of the present invention; FIG. 2 is a schematic chart showing electron energy levels for the first four shells of an atom indicating the number of whole waves contained in the subshells' orbits according to the model of the present invention; FIG. 3 is a perspective view of one embodiment of the invention for representing the p orbitals of an atom; FIG. 4 is a perspective view of the prior art model for representing the p orbitals of an atom; FIG. 5 is a plan view of one embodiment of the invention for representing a composite model of the first three shells of an atom; FIG. 6 is a plan view of one embodiment of the invention for representing the fourteen electron f orbitals of an atom; FIG. 7 is a plan view of the arrangement of the current loop magnetic fields of another embodiment of the present invention; FIG. 8 is a plan view of a magnetic model of the present invention for representing a group of five magnetic elements arranged to define a sphere; FIG. 9 is a plan view of a magnetic model of the present invention for representing the combined s and p subshells or the octet configuration for an atom. FIG. 10 is a perspective view of a magnetic model of the present invention for representing the d orbitals of an atom; FIG. 11 is a plan view of a magnetic model of the present invention for representing the f orbitals of an atom; FIG. 12 is a plan view of a magnetic model of the present invention for representing a composite third shell of an atom; FIG. 13 is a plan view of a magnetic model of the present invention for representing a composite fourth shell of an atom; FIG. 14 is a plan view of a model for representing benzine rings; FIG. 15 is a perspective view showing the driving support for the model shown in FIG. 9 FIG. 16 is a plan view of a composite model consisting of four submodels representing the fourteen circle f orbital forms. The new model of the atom can best be examined by reference to a hydrogen atom represented by FIG. 1 in which the single s electron orbits in an equatorial path 1 around the proton nucleus 2. Since the single electron surrounds the nucleus in an equatorial manner with the freedom to precess there is no detectable angular momentum and accordingly 1=0. In FIG. 1 the paths 3, 4 and 5 shown in dotted lines indicate that the electron is free to move about the nucleus 2 while precessing with no preferred direction or axis of orbit. Here the electron is at the first energy level or ground state where n = 1 and defines the spherical surface 6. In accordance with de Broglie's standing wave theory, the is orbit of the single s electron in this shell would be one wavelength. If the electron defining this path were to receive energy from an outside source, as from a collision or an entering photon of sufficient energy, the electron would be raised to a higher energy state. The preferred transition according to spectroscopic evidence would be to the 2p state in this case. Previous models would represent this 2p orbital as an ellipsoidal charge cloud extending as a lobe outwardly from the nucleus; however, in the new model, the circular is orbit when deflected by the incoming energy is moved along the axis of rotation it possesses at that instant, for example in, and raised above the nucleus to the second energy level or shell 2. In this position, it occupies a meridian cap 8 defining the 2p orbital on the second shell energy sphere. This occupancy normally lasts less than 10-8 seconds before the electron returns to the s state with the emission of the characteristic first line of the Lyman hydrogen series. According to the new model then, the orbit of the 2p state is a one-wave orbit similar to the s orbit with the difference that it is displaced to the second shell. As a consequence of its displacement away from the nuclear center, the orbit acquires a direction in space in reference to the nucleus and because this includes a detectable directional axis 8a, it now has a detectable angular momentum vector. As shown in FIG. 1, the 2s orbital 9 in the new model would be an equatorial orbit, and in accordance with the earlier Bohr-de Brogue model, this 2s orbital would have a standard two-wave cycle as shown diagrammatically in FIG. 2. Also, as shown in FIG. 2, the second shell 7 would for purposes of constructing the new model be made up of two subshells 7a and 7b with subshell 7a containing the 2s orbitals and subshell 7b containing the 2p orbitals. It is important to note here that the electron's de Broglie wave length is dependent on the linear velocity of the electron, and is given by the formula pastedGraphic.pdf ¬=h/mv where h=Plank's constant, m=the mass of the electron and v= the velocity of the electron. In restricting the 2p electron of the second shell to complete its orbit in but one standing wave, the new model implies that the linear velocity of the electron is substantially the same for both the 2s and 2p orbitals. Therefore, the electron's wavelength is substantially the same. The difference is that the electron in an orbit of just one wave will complete its orbit in half the time required for the orbit with two waves. As will be shown below, this size reduction from the standard s orbital to the smaller offset state represents the differences in angular momentum for the various types of orbit s, p, d, and f of the same shell. Referring again to FIG. 2, the third shell of the atom is shown diagrammatically as made up of three subshells 10a, 10b, and 10c since the third shell requires three types of orbitals, 3s, 3p and 3d where l =0, 1 and 2, respectively. Extending the deflected orbit hypothesis to this third shell, the normal Bohr-de Broglie three-wave orbit 11 representing the 3s orbital is shown as surrounding the nucleus 2 in an equatorial manner while the 3p and 3d orbitals are shown at 12 and 13, respectively as offset from the nucleus. Since the maximum number of waves possible in the normal third shell orbit is three, the offset states or contracted orbits can contain two waves or alternatively, one wave. As discussed earlier, the orbit which is formed in this way will have the same linear velocity as the s orbital of that shell. Therefore, the electron which completes the two-wave cycle 12 on the energy surfaceb 10s of the third shell will complete each cycle half again as fast as it would in the three-wave orbit. If the size of the electron's orbit is further reduced in the third shell by an energy interaction it can achieve the one-wave orbit 13 and complete its cycle twice as fast as it does in the two-wave orbit. This accelerated rotation results in an increase of angular momentum just as if the revolutions of a gyroscope were accelerated. Therefore because the 3d orbital has twice the angular momentum as the 2p state, the one-wave orbit must be the 3d, orbital 13, and the two-wave orbit must be the 3p, state 12. It can now be seen that in the new model, each shell begins with its appropriate equatorial Bohr-de Broglie orbit which contains the same number of waves as the principal quantum number, n= 1, 2, 3, 4 etc. while each shell also has (n=1) additional types of deflected states containing successively fewer standing waves, the minimum for any orbit being one wave. Extending the pattern to the fourth shell of the atom which as shown in FIG. 2 is made up of four subshells 14a -14d, the four-wave equatorial orbit or 4s state shown at 15 contains four waves while the three-wave deflected state shown at 16 represents the 4p orbital, the two-wave deflected state shown at 17 represents the 4d orbital, and the one-wave deflected state shown at 18 represents the 4f orbital. It is necessary for a proper atomic model to account for the motion and spatial occupancy of all electrons of all energy levels for even the heaviest atoms. This may require accounting for over 100 electrons. Such a building-up system is a unique aspect of this new model. In conventional models, the s orbital structure includes two electrons occupying a spherical shell with opposed spins. Nothing here is changed in this new model. Such a subshells are constructed in each new shell. Because they are spherically symmetrical and have no preferred orientation, each s electron pair or subshell can advantageously be represented simply by a transparent sphere of plastic or similar material. In building up an atom according to the periodic table and Pauli's Exclusion principle, the second shell accommodates a pair of 2s electrons outside of the 1s pair of electrons. This pair defines subshell 7a of the second shell as shown in FIG. 2. Six more electrons in p orbitals 8 must he added, however, in order to complete the second shell. In accordance with the unique properties of this new model, these p orbitals do not penetrate the inner shells nor do they extend or overlap one another's domains. As shown in FIG. 3 they are represented by six identical circle ring members 19 defining offset circular orbits, the six of which are arranged along x, y, z axes of the atom in the same way as the electrons of the ellipsoidal charge clouds of the conventional model shown in FIG. 4. It will be noted from FIG. 3 that, as a dimensional characteristic of the model there shown, the diameter of the open circular area between adjacent ring members 19 is less than the diameter of the ring members themselves. This circular area is shown in FIG. 3 by the dotted line 19. These six circle rings as shown in FIG. 3 constitute a p subshell 20 which may net only be used to represent the 2p subshell 7b of the atom but may also be used for representing the 3p and 4p subshells since the only difference between these subsheils is in their relative size and the wave cycling of the p electrons and for purposes of model shown in FIG. 3, relative size and the representation of the electron waves have been omitted. It is to be understood, however, that appropriate wave paths can be drawn on the circles 19 for purposes of instruction and the like if desirable, and that a series of p orbital models like that shown in FIG. 3 can be made with appropriate dimensions when for example it is desired to use the 2p, 3p and 4p subshells at the same time. In the third completed shell of the atom, the 3s subshell 1Oa is shown in FIG. 5 as a sphere completely surrounding the 2p subshell 7b and positioned at the appropriate distance from the nucleus of the atom whereby three standing waves may exist. The 3p subshell lOb surrounds the 3s subsbeil at the same effective energy level and as indicated above, it will be composed of six two-wave circular orbits which are arranged on a spherical surface similar to the 2p subshell 7b. The next subshell which completes the third shell is the 3d subshell lOc which surrounds the 1Oa and 1Ob subshells at the same effective energy level, and as shown in FIG. 5 by the circle rings 21, comprises a group of ten d electron orbitals. FIG. 2 shows that each of the d electrons in the 3d snbshell will define single standing wave 13. In a model of the fourth shell of the atom, the sphere 14a shown in FIG. 2 would surround the 3d subshell 1Oc of FIG. 5 and be surrounded by the six 4p three-wave orbitals 16, the ten 4d two-wave orbitals 17, and the largest of the subshells, the fourteen 4f one-wave orbitals 18. For purposes of illustration the construction of this latter subbshell is shown separately in FIG. 6 where rings 21 are used for representing the fourteen 4f orbitals. In this manner the building process can continue on to account for the total number of electrons required of even the heaviest atoms in the periodic table. In all of the representations of electronic motion in these new models, one fact should be observed. In none of the orbits is an electron required to move inwardly or outwardly from the nucleus as in the elliptical charge clouds of previous models. Each electron remains at a constant distance from the nucleus and hence, in a constant electrical potential. Only in changes from one state to another would the electrons jump through varying nuclear electrical potentials. Therefore, the model shows that the emission or absorption of energy requires electrical work to be performed by an electron's movement through a potential difference. Referring again to the four quantum numbers, the m or magnetic number is now accounted for by the direction in which the orbits face relative to one another in any of the offset shell groups, and the spin number s has in the new model gained a logical reference to the m number and it is possible for the first time to visualize with certainty whether spin is in the same or opposite direction as the electron's motion in orbit. As described above, pairs of s electrons follow one another around the nucleus of the atom so that their spin magnetic fields are related one to the other like two permanent magnets fixed in space. Since, however, the electrons in subshells with offset p, d, and f orbitals do not follow one another along the same motion course, their spin fields are smeared with respect to one another and diffused over the entire path of the orbit. In addition to spin magnetic fields, the electrons also possess a separate orbital magnetic moment arising out of the orbital motion of the electrical charges. This orbital magnetic moment is identical to the magnetic field of an electric current loop and lies perpendicular to the plane of the orbit with the north pole on one face and the :south pole on the other. Its value is assigned with the l quantum number since the quantity of orbital magnetism depends directly on the angular momentum of the orbiting electron. There is an important relationship between the two types of magnetic field since the electron can arrange its spin in either the same direction or the reverse of its direction of rotation in orbit. This means that spin can either add to, or counter the orbital field. As will be described, below, this mechanism can function as a device for cancelling the magnetic fields under certain conditions. If the kinetic energy of the electron is great, as it is for the inner shells of the heavier atoms, the orbital magnetic fields are also very great. In the first shell of calcium, for example, the magnetic moment is about loss gauss per electron, and in the first shell of uranium about 1010 gauss. Forces of this magnitude inside the atomic shells must be dispersed in some way. Yet in all of the considerations given to atomic structure in previous models it is nowhere evident that a useful purpose is expected of these forces. In the past there has been much discussion concerning the coupling of the magnetic currents within the atom but no indication of the internal form which this coupling might assume. According to the teachings of the present invention, a model of the atom showing this magnetic coupling may be constructed by replacing the circle rings of FIGS. 5 and 6, for example, with magnets 22 having the same shape and polar arrangement as the field of current loops. These magnets may be made of ceramic material and are shaped like fiat washers polarized on opposite faces. Flat magnetic fields attract one another in two different attitudes. When their polar directions are identically oriented or parallel, they attract face to face, and when their poles are reversed to one another or antiparallel, they attract edge to edge. As shown in FIG. 7, this antiparallel association permits complete freedom in the range of angles at which any two magnets can associate. The edge to edge association is of special importance for it may be employed in constructing models to represent the magnetic coupling of atomic orbitals. As shown in FIGS. 8-13 it is possible to assemble certain groups of the magnets 22 around a sphere in a mosaic of antiparallel fields to represent the electrons of the different shells and subshells of the atom. In FIGS. 8-13 it will be noted that touching magnets have their magnetic fields disposed in antiparallel relationship in the same manner as shown in FIG. 7. Each of the magnets of these models may be placed on non-magnetic armatures 23 in order to support their weight and when they are in the proper antiparallel position they cling together. They can be withdrawn individually and when returned, they are seized by the neighboring magnets. Each of the groups is linked together in closed spherical circuits. As completed forms, they define patterns of alternating polarity so that there is no preferred magnetic direction for the represented electron shell. This is in agreement with all experimental evidence which shows that angular momentum and magnetism add to zero for completed shells of electrons. There is a remarkable correspondence between the numbers of spherical circle groups which can be as- 2 sembled from magnets and the numbers of electrons in energy levels. If magnets of the same diameter are used in forming any one of the spherical groups of FIGS. 8-13 and the diameter of the open circular area between any four adjacent magnets is smaller than the diameter of one of the magnets, as for example as shown in FIG. 11 at 22', only certain groupings are possible. More specifically, it is only possible to form spheres having five, eight, ten, fourteen, eighteen and thirty-two magnets and these are shown respectively in FIGS. 8-13. Other combinations cannot be made with magnets because of the magnetic field relationships presented. It is to be noted that these numbers correspond closely to the number of electrons present in the first four completed shells and associated subshells of the atom. The notable exception is the group of five magnets shown in FIG. 8 which is the smallest assembly possible. Although this does not represent a completed energy level of the atom, it can be used for representing the sp2+p hybrid orbitals; and the group possesses the useful property of linking with other groups of five to form hexagon rings with perfect magnetic continuity. An assembly of these groups which contains six of the five magnet forms would seem to require thirty magnets. It is found however that each two adjacent groups when joined, can share a magnet which is their common face. This cancels six magnets so that a hexagonal ring may be formed with a total of twenty-four magnets and an average of four rather than five to a cell. Such a hexagonal assembly is shown in FIG. 14 and if each magnet is thought of as an electron in orbit the assembly becomes an excellent model of the benzine ring of organic chemistry. For here is a flat hexagonal ring of atoms which can be repeated in an extended pattern like a collection of aromatic ring molecules; and as a model, each carbon atom has the proper number of outer electrons, four, to represent an electrically neutral molecule. This configuration offers a reasonable explanation for the long debated question of organic chemistry regarding the actual structural make-up of the benzine ring which was usually justified in terms of alternating or delocalized bonds in order to account for the proper number of electrons in each carbon atom. The magnet models shown in FIGS. 9, 12 and 13 contain the sets of numbers for the completed second, third and fourth shells of the atom while the models of FIGS. 10 and 11 contain the sets of numbers for the d and f orbitals. Absent from the group is the six-circle cubical set which would be expected in order consistently to represent the p subshell. Magnetic coupling is prevented in this arrangement because there is no way in which the six faces of a cube can be checkerboarded to permit the association of opposite magnets. The only completely symmetrical organization for this form is an arrangement in which all six magnets face outwardly with the same polar orientation. In terms of magnets, this is a parallel or repelling association. In an atom this orientation of magnetic fields would add to the electrical repulsion between the electrons and force them into a higher energy state. If this happens to take place in an outer shell where the kinetic energies of the electrons are small, it is possible for spin to neutralize the orbital magnetic fields by reversing its orientation. This would tend to cancel the repelling force of the orbital magnetic fields and permit the electrons to approach one another more closely and thus reach a somewhat lower energy state. The electrons in the inner shells have higher kinetic energies and greater orbital magnetic moments. Because spin is a constant it cannot serve to neutralize these larger orbital fields. According to the teachings of the present invention, it is necessary in 'constructing magnetic models of the heavier atoms for the p electrons of the inner shells to combine with the s electrons of those shells in order to form the single magnetic configurations of eight identical orbits as shown in FIG. 9. This is reasonable since the s orbitals beyond the first shell have only a provisional chemical stability and do not represent a tightly closed system. This eight-circle group of FIG. 9 is arranged on a spherical surface along the corner axes of a cube. The four circles whose north poles face outwardly alternate with the four whose south poles are exposed with the two sets describing interlocking regular tetrahedra. Although the octet of the inert gases is generally believed to comprise an s subshell and a p subshell, there is some controversy regarding this. Linus Pauliag and others have discussed the possibility that s and p shells are a single entity like two interlocking tetrahedra. The model of FIG. 9 supports this latter view of a single octet shell and in addition, may be used to show such structures as theH2Omolecule with the two lower forwardly facing discs representing the two hydrogen atoms bonded to the Oxygen atom at 1090 28’. In assembling the models of FIGS. 9-13, the armatures 23 may be connected to a suitable framework 24 adapted to be disposed in the interior of the spheres. FIG. 15 shows such a structure for mounting the model of FIG. 9 in which eight magnets 22 are to be assembled. As there shown the framework 24 has secured thereto at proper points the eight armatures 23 upon which the magnets 22 are to be placed. In the support shown in FIG. 15, the bottom armature is magnetically connected to a suitable magnetic turntable 25 driven by a motor 26. In this way, the lower magnet of the model as shown in FIG. 15 becomes the driving disc for the remaining magnets which are placed on their respective armatures for free rotation; and when the driving disc or magnet is actuated, the entire set of magnets will rotate with all north poles turning in one rotational sense and all south poles in reverse as indicated by the arrows in FIG. 9. This causes no change in the relationship of the magnetic fields since the north and south poles remain constant to one another. The magnets simply act like a set of gears, spherically arranged and in frictional contact. This phenomenon, which can be attributed to binary systems, that is, the pairing of the magnets shows an important principle. For what is observed here, in mechanical form, has its exact counterpart in electricity where two orbits or electrical loops must have counter-rotating charges in order to give rise to antiparallel fields. In addition to the individual models shown in FIGS. 8-13, it is within the teachings of the present invention to translate the groups of the models in space, cell upon cell like polyhedra and to combine various types of models into a composite model with no loss of magnetic or gearing continuity. For example, FIG. 16 shows an assembly comprising four fourteen-circle magnetic groups arranged in a square. This system can be translated in space with the polarities of the adjacent groups providing the proper magnetic linkage from cell to cell. By turning one magnet of a group, an endless assembly can be made to turn like an infinite system of gears and in all the various forms a structural order of great intricacy can be seen. For example, a complex model can be constructed for representing various crystalline lattices composed of electron networks magnetically arranged and bound by nuclear charge centers. The above description includes a number of examples of models and the manner in which they may be assembled and used to represent various atomic forms; however, it is to be understood that various changes may be made without departing from the spirit of the invention as set forth in the following claims. What is claimed is: 1. A model for atomic forms comprising a plurality of substantially identical circular disc magnets polarized on opposite faces and arranged in a group defining the boundary of a sphere with each magnet making edge contact with at least two other magnets and having its outwardly exposed surface of a polarity opposite that of each contacting magnet. 2. A model for atomic forms as set forth in claim 1 in which the diameter of the open circular area between any adjacent magnets is less than the diameter of said magnets. 3. A model for atomic forms comprising a plurality of concentrically arranged spheres for representing the different energy levels of an atoas with each represented energy level including at least one sphere comprising a plurality of circular members having predetermined equal diameters and arranged in a group to define that sphere with the periphery of each member engaging the periphery of each adjacent member and lying in separate planes on that sphere offset from planes extending through the center of the model. 4. A model for atomic forms as set forth in claim 3 in which the diameter of the open circular area between adjacent circular members defining any sphere is less than the predetermined diameter of the members of that sphere. 5. A model for atomic forms as set forth in claim 4 in which the circular members are disc magnets polarized on opposite faces and arranged with each magnet making edge contact with at least two other magnets and having its outwardly exposed surface of a polarity opposite that of each contacting magnet. 6. A model comprising a frame member, a plurality of support rods extending outwardly from a common point in said frame, substantially identical circular members having predetermined equal diameters rotatably mounted on said support rods about said frame with each member extending in a plane at right angles to the longitudinal axis of its support rod, said rods being positioned on said frame whereby said circular members define a sphere with each member making edge contact with at least two other members and with the diameter of the open circular areas between any adjacent magnets being less than the predetermined diameter of said magnets, and means for rotating one of said members. 7. A model comprising a frame member, a plurality of support rods extending outwardly from a common point in said frame, substantially identical circular disc magnets polarized on opposite faces and having predetermined equal diameters rotatably mounted on said support rods about said frame with each magnet extending in a plane at right angles to the longitudinal axis of its support rod, said rods being positioned on said frame whereby said magnets define a sphere with each magnet making edge contact with at least two other magnets and with each magnet having its outwardly exposed surface of a polarity opposite that of each cootactiing magnet, and means for rotating one of said magnets. 8. A model as set forth in claim 7 in which the diameter of the open circular area between any adjacent magnets is less than the predetermined diameter of said magnets. References cited by the Examiner 2,167,641 8/1939 Dewan ----------------------------74-210 FOREIGN PATENTS 55,975 6/1952 France. EUGENE R. CAPOZIO, Primary Examiner. H. S. SKOGQUIST, Assistant Examiner. UNITED STATES PATENT OFFICE CERTIFICATE OF CORRECTION Patent No. 3,276,148 October 4, 1966 Kenneth D. Snelson It is hereby certified that error appears in the above numbered patent requiring correction and that the said Letters Patent should read as corrected below. Column 1, line 15, for "electron's" read -- electrons' --; line 22, for "minature" read -miniature --; column 2, line 12, for "De Brogue" read -- de Brogue --; line 45, for "anular" read -- angular --; column 3, line 18, for "1" read -- 1 - -; line 25, the formula should appear as shown below instead of as in the patent: column 4, line 63, for "have" read -- having - -; column 5, line 2, after "f", in italics, strike out the comma; same line for "subshell" read -- subshell. --; column 7, line 72, for "weave" read -- wave -- column 8, line 6, for "an" read - - any - -; line 38, for "1" read - - Signed and sealed this 29th day of August 1967. (SEAL) Attest: ERNEST W. SWIDER Attesting Officer EDWARD J. BRENNER Commissioner of Patents Кушелев Снельсону Кушелев: Наши ГЕОМЕТРИЧЕСКИЕ модели электронных оболочек атомов и многих молекул полностью совпадают. Kushelev: Our GEOMETRICAL models of electronic covers of atoms and many molecules completely coincide. Тем не менее у Огжевальского, Снельсона, Кушелева, Кожевникова, Соколик ... есть уникальные модели, которые дополняют модельный ряд других авторов. И в этом наша сила Nevertheless at Ogzhevalsky, Snelson, Kushelev, Kozhevnikov, Sokolik... there are unique models which supplement a model range of other authors. And in it our force Кроме того, у Огжевальского и Кушелева есть модели нуклонов, которые в первом приближении тоже имеют форму кольца. Besides, at Ogzhevalsky and Kushelev there are models of nucleons which as a first approximation too have a ring form. Однако мои модели кварков проработаны на уровне 2 и более уровней структуры... However my models of quarks are worked at level of 2 and more levels of structure...
Дорогой Кен! Различие между нашими моделями появляются на уровне процессов. Я и Огжевальский рассматривали самоорганизацию волноводов в радиоэфире. Это уже не геометрический, а физический уровень модели. На этом уровне фотон представлен волной в волноводе, а электрон - волна в закольцованном, т.е. в замкнутом волноводе. Но это только самая жёсткая часть системы. Чтобы кольцо не размыкалось, нужны "спицы", как в велосипедном колесе. Роль спиц выполняет электрическая, упругая и магнитная деформации кристаллоподобного эфира. Переход от формы элементарных частиц к форме и взаимному расположению элементов эфира - это переход из микромира в наномир. Переход от пикотехнологии к Планк-технологии (10^-35 метра). На эту тему есть статьи на английсом языке: Autotranslation: Dear Ken! Distinction between our models appear at level of processes. I and Ogzhevalsky considered self-organizing of wave guides in radio-ether. It is not so geometrical, and physical level of model. At this level the photon is presented by a wave in a wave guide, and an electron - a wave in girdled, i.e. in the closed wave guide (circle). But it is only the most rigid part of system. That the ring wasn't disconnected, "spokes", as in a bicycle wheel are necessary. The role of spokes carries out electric, elastic and magnetic deformations of kristalic ether. Transition from a form of elementary particles to a form and a relative positioning of elements of ether is a transition from a microcosm in a nanoworld. Transition from a pikotech to Planck-tech (10^-35 meter). On this subject there are articles in angliysy language: 1. http://www.nanoworld.org.ru/data/01/dat … 900505.htm и другие / and other: http://www.nanoworld.org.ru/data/01/dat … /index.htm Общее оглавление текстов (до 2004) / General content txt-arj:http://www.nanoworld.org.ru/data/01/dat … exteng.htm Оглавление архива рассылки (по-русски) / Content subscrybe-arj (russian):http://nanoworld88.narod.ru/data/ Копия форума 2006-2012 (forum copy): http://nanoworld88.narod.ru/forum/index.htm *** Письмо Кеннету Снельсону (2012-04-22)
Кушелев: Число витков определяется из отношения магнитных моментов протона и нейтрона Kushelev: The number of rounds is defined from the relation of the magnetic moments of a proton and a neutron... 22.04.2012, 00:58, "kenneth snelson" <k_snelson@mac.com>:
Авиалайнер «Боинг-737» упал на деревню недалеко от аэропорта Исламабада *** Вести c ускорителей и не только! Сапфировый шар диаметром 65 мм доставлен в Дмитров. Началась настройка измерительного тракта Сферический резонатор установлен на пенопластовую подставку с цилиндрическим отверстием. Использование приёмной и передающей четвертьволновых антенн не помогло обнаружить резонансов сапфирового шара в диапазоне от 1.78 до 2.56 ГГц. Придётся делать переходники на диэлектрические волноводы... Учитывая, что в Дмитрове часто отключают электричество, придётся использовать блоки бесперебойного питания не только для компьютеров, но и для измерительных приборов. Иначе можно испортить приборы и эксперимент затянется на неопределённый срок...
Добротность колебательной моды 2HE без экрана очень мала, поэтому её не удастся измерить даже с помощью диэлектрических волноводов. Придётся сначала сделать экран, повышающий добротность колебательной моды 2HE... http://jre.cplire.ru/win/apr06/2/text.html
В случае идеального экрана при определенных параметрах резонатора для колебания Е102 была получена добротность равная 10^10 (рис. 7). Это было достигнуто уменьшением толщины слоя и потерь в нем, что повышает добротность, а также выбором оптимального положения экрана. При удалении экрана было обнаружено два максимума, причем дальний из них по отношению к диэлектрику значительно превосходит ближний по добротности. При введении небольших потерь в экран картина качественно сохраняется.
Скрипт для 3DS Max: el = #() Твёрдый "орешек" Пикотехнология белков, ДНК, РНК
Инвестор купил пластиковые кольца для сборки пикотехнологических моделей. Теперь нужно найти помощников, которые помогут быстро собрать ключевые фрагменты пикотехнологических моделей белковых молекул.
Эх, если бы такое же количество было мышей, то эликсир "вечной молодости" мы создали бы "в два счёта" Материал с форума лаборатории Наномир:diprospan: интересно, какой алгоритм заложил Jonatan Ellis в свою новую версию ( 0.6.2 ) программы Marwin.A program to aid crystallography construct design http://pypi.python.org/pypi/marvin/0.6.2 Marvin is a program to help design protein constructs and generate PCR primers. https://github.com/jjellis программу он позиционирует как Предсказатель структур белка. на входе программе нужен нуклеотидный файл формата FASTA. программа бесплатная GNU General Public License (GPL) интересно тут то, что австралиец Джонатан Эллис, из Брисбена, выкладывает свою программу с исходниками, пишет на Питоне, т.е. есть версии для всех существующих платформ. версия для Windows: https://github.com/downloads/jjellis/ma … -0.6.2.exe   Кушелев: Очень интересно. Давайте посмотрим алгоритм. Может быть он тоже открыл, в смысле, переоткрыл композиционный генетический код? Композиционный код:
Код вполне реального белка. Структура вполне осмысленная. Приглашение к сотрудничеству для людей умеющих самостоятельно мыслить; не просто умных, а мудрых, которые чувствуют, где истинаЛаборатория Наномир готова к любому взаимовыгодному сотрудничеству. У нас есть сторонники как явные, которые помогают морально и материально, есть очень много пассивных наблюдателей, есть и ярые противники, которые используют любые методы и средства (аморальные и просто преступные), чтобы уничтожить работу лаборатории и дискредитировать ее. В одиночку внедрить технологии, выводящие цивилизацию на новый уровень, невозможно. Благодаря поддержке множества заинтересованных людей проделана огромная работа. Ознакомиться с её результатами можно изучив материал рассылки "Новости лаборатории Наномир". Люди науки могут изучить научные труды. Вклад каждого не останется незамеченным в случае успеха в реализации научных проектов. Результаты совместной деятельности принадлежат участникам проекта пропорционально коэффициентам творческого и финансового участия. Основные разработки: Микроволновый источник энергии В 2011 году были куплены рубиновые шарики для эксперимента на сумму ~1000 долл. В результате было сделано научное открытие, проверена защита диэлектрических резонаторов от перенапряжения. В этом году, вероятно, можно будет создать микроволновую энергетику, т.к. удалось найти сырьё (рубин #8), из которого сделаны рубиновые шарики для эксперимента в Дубне. Параллельно началась серия экспериментов на ускорителе "B" в диапазоне 20 ... 140 ГГц. "Эликсир вечной молодости" 28 сентября 2011г. в институте геронтологии (г.Киев) начался эксперимент по созданию "эликсира вечной молодости". Благодаря первому взносу (в размере 500 долларов) Золдракса и поддержке других соинвесторов. Продолжаются переговоры с потенциальными инвесторами по поводу финансирования этого проекта. Программа исследований Презентация Пикотехнология Созданы первые версии пикотехнологии (выпуски рассылки 212 270 271 272 ), с помощью которой Александр Кушелев и Виктория Соколик сделали более10 научных открытий. Виктория Соколик: Уважаемые коллеги, Вашему вниманию предоставляется услуга -- моделирование 2D и 3D структуры любого белка без ограничений в его размере и степени изученности с помощью программного обеспечения, базирующемся на принципиально новом подходе декодирования нуклеотидной последовательности, детерминирующей данный белок. Всё, что необходимо от заказчика, это нуклеотидная последовательность мРНК интересующего его белка (или код этой нуклеотидной последовательности в EMBL, или хотя бы код самого белка в PDB). В течение 1-3 суток мы готовы предоставить Вам схему вторичной структуры заказанного белка (2D), модель его пространственной структуры (3D) в виртуальном пространстве, а также файл .pdb с координатами каждого атома белка. Файл .pdb может быть использован по аналогии с файлами закристаллизованных белков из PDB банка для дальнейшего конформационного анализа белка методами молекулярной динамики с учётом физико-химической специфики микроокружения белка или его взаимодействия с лигандами. Таким образом, Вы сможете максимально быстро удобным для Вас способом (по электронной почте, на сайте либо на электронном носителе) получить информацию о структурном шаблоне Вашего белка. Первые 10 заказов -- бесплатно . Цена следующих заказов -- договорная. Сотрудничество может быть различным: - участие в научных дискуссиях на форуме (конструктивное) - совместное создание коммерческого продукта - поиск инвесторов - выступить менеджером по продаже готовых коммерческих продуктов - конструктивные предложения по продвижению идей лаборатории Наномир - содействие в проведении экспериментов
и т.п. - написание совместных научных статей и т.п. - материальный вклад (денежный или обеспечение оборудованием и материалами)
Пожалуйста, сообщайте о своем вкладе, чтобы мы зачли Вас как партнера лаборатории Наномир. +7-926-5101703, +7-903-2003424, +7-916-8265031, Skype: Kushelev2009, mail: kushelev2011@yandex.ru веб-мани: WM-кошелек R426964799301 Другие способы перевода
|
| В избранное | ||