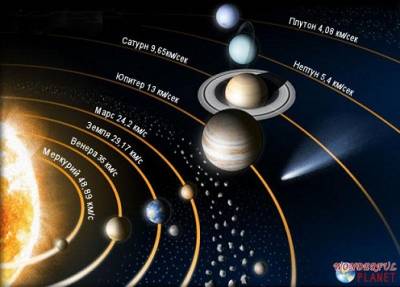
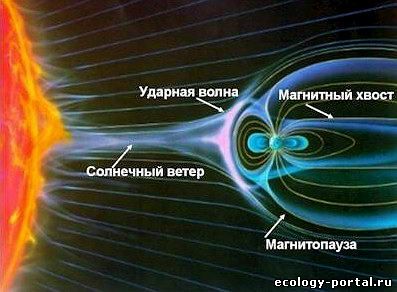
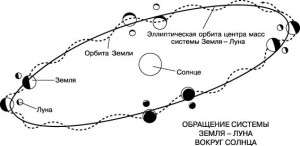
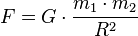| ← Июнь 2015 → | ||||||
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|---|---|---|---|---|---|---|
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
|
22
|
23
|
25
|
26
|
27
|
28
|
|
|
29
|
30
|
|||||
За последние 60 дней ни разу не выходила
Сайт рассылки:
http://gravitus.ucoz.ru/
Открыта:
10-05-2014
Адрес
автора: media.news.gravitus-owner@subscribe.ru
Статистика
0 за неделю