Отправляет email-рассылки с помощью сервиса Sendsay

Сдай ЕГЭ и ЕНТ по математике на отлично!

Подписаться Бесплатная «Серебряная» новостная рассылка . Подписчиков 746 RSS
←   Апрель 2011   →
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


За последние 60 дней ни разу не выходила


Открыта: 09-06-2007

Автор
Салимжанов Рафик Михайлович

Статистика

746 подписчиков
0 за неделю
←   Все выпуски   →

Решения тестов ЕГЭ по геометрии


Сдай ЕГЭ и ЕНТ по математике на отлично!. ВЫПУСК 51
Рассылка сайта Сдай ЕГЭ и ЕНТ по математике на отлично!
ЗДРАВСТВУЙТЕ! В СЕГОДНЯШНЕМ ВЫПУСКЕ:
  • Новости сайта
  • Тесты ЕГЭ и ЕНТ
  • Анекдот
  • Дружественные рассылки

    • Новости сайта

    Всего подписчиков в "Рассылках@Mail.Ru": 3569 , а на SUBSCRIBE.RU - 1027.

    В архиве рассылки можно ознакомиться со всеми предыдущими выпусками.

    Вот закончилась третья четверть учебного года. Настала пора усиленной подготовки учашихся к выпускным экзвменам.

    Конечно, если ты живешь в большом городе, то купить пособия для подготовки к выпускным экзамена не проблема, только были бы деньги. Для всех остальным своевременная покупка таких материалов большая проблема, осбенно для тех, кото живет вне Россиию Поэтому многие начинают искать материалы для подготовки к ЕГЭ-2011 в Интернете. Чтобы помочь я публикую некоторые адреса бесплатных электронных библиотек, к услугами которых я и сам нередко пользуюсь.

    http://www.all-ebooks.com/ - библиотека электронных книг. Чтобы быстро найти нужные книги,например, по математике лучше в строке поиска по сайту набрать слово "математика".
    http://www.bookdownloads.ru/ - портал BookDownloads.ru. Здесь можно найти книги на все случаи жизни.
    http://www.bookshunt.ru/index.php - универсальная библиотека DataHunt
    http://www.booksgid.com/- библиотека Books Gid
    http://bookarchive.ru/ - библиотека BooksArchive.RU

    Кроме этого предыдущем номере этой рассылки (http://content.mail.ru/arch/27136/7270073.html) я опубликовал адреса для скачивания вариантов и Рабочих тетрадей C1 - C6 для подготовки ЕГЭ по математике.
    Тесты ЕГЭ и ЕНТ

    В предыдущем номере в Заданиях для самостоятельного решения по моей вине в ответах воторого примера были допущены ошибки. Публикую полность исправленное это задание .

    2. Решите уравнение: |5x2 - 3| = 2.

    А) -5; √3; -√3; 5
    В) -4; -1/(2√5); 4; 1/(2√5)
    С) -1; -1/(√5); 1; 1/(√5)
    D) -2; -1/(√14); 2; 1/(√14)
    Е) -3; -1/(2√7); 3; 1/(2√7)

    Рад сообщить, что этот раздел рассылки я сегодня веду вместе с учеником 9 класса Первой гимназии г. Петропавловска республики Казахстан Холоповым Максимом. Он тоже является большим специалистом в поиске "особых" решений тестов несколькими ответами для выбора правильного среди них.

    Решения геометрические задания в тестах ЕГЭ очень часто вызывают затруднения у школьников. Поэтому сегодняшняя рассылка посвящена некоторым тестовым заданиям ЕНТ с геометрическим содержанием.

    Пример 1. Найти длину высоты прямоугольного треугольника, опущенной из вершины прямого угла, если она делит гипотенузу на отрезки, равные 3 и 27 см.

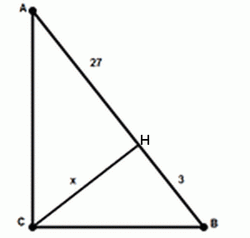    рисунок Решение I. Известно, что высота х в прямоугольном треугольнике, проведенная к гипотенузе равна среднему пропорциональному отрезков длиной 3 и 27. Поэтому х = √3х27 = 9.

    Решение II.

    По теореме Пифагора, найдем катеты АС и СВ.
    В треугольнике AHC : AC2 = 272 + x2.
    В треугольнике CBH : CB2 = 32 + x2.
    AC2 + CB2 = AB2
    2x2+272 + 32 = 302
    2x2=900 - 729 - 9
    x2=81

    x = 9. То есть, длина искомой высоты - 9 см.
    Ответ: 9 см.

    Пример 2. Найдите площадь правильного треугольника, если площадь вписанного в него круга равна 16π см2

    Решение.

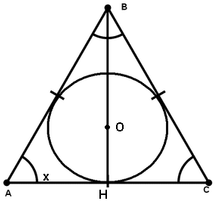    рисунок Так как площадь круга вычисляется по формуле πR2, то исходя из данных не трудно найти радиус этого круга. Его длина равна 4 см. Так как треугольник правильный, то BH=3OH =12 см.

    Итак, высота найдена. Для вычисления площади треугольника нам осталось найти длину стороны, к которой проведена высота. Пусть AH = х. Т.к. АН лежит против угла в 30о, то она равна половине гипотенузы AB треугольника АВН. Значит, AB = 2x. Тогда, по теореме Пифагора:

    4x2 = x2+144, 3x2 = 144, x2 = 48, x = 4√3.

    BH-медиана к стороне AC, значит AC = 2AH = 8√3. Отсюда легко находим площадь треугольника. Она равна половине произведения BH и AC, т.е. 48√3 см2.

    Ответ: 48√3 см2

    Задачи для самостоятельного решения
    1. Высота, опущенная на гипотенузу прямоугольного треугольника делит его на два треугольника, площади которых соответственно равны 6 см2 и 54 см2. Найдите гипотенузу треугольника.


    2. Длина окружности, вписанной в правильный треугольник равна 16π см. Найдите площадь такого треугольника.

    Если вы не хотите пропустить свежие номера этой рассылки, то подписывайтесь на нее по адресу http://content.mail.ru/pages/p_27136.html и посоветуйте это сделать своим друзьям. Для этого просто перешлите им это письмо.

    Всё ли в ней устраивает, или можно что-то подправить? Буду рад услышать Ваши пожелания и предложения. Щелкните здесь и напишите мне.
    Напоследок анекдот

    - Почему ты плачешь, Вовочка?
    - Мама сказала папе, что он слон. Папа ответил маме, что она курица.
    - Ну и что?
    - А кто же тогда я?!
    Дружественные рассылки

    1. Учительница информатики - работаем с удовольствием!.
    Если у вас есть интересные тестовые задания, трудные математические задачи или вы просто не можете решить тестовое задание или математическую задачу, присылайте ее в рассылку или на Форум, решим вместе!

    ОБРАТНАЯ СВЯЗЬ:

    1. E-mail автора рассылки: щелкните здесь
    2. Форум ЕГЭ и ЕНТ в вопросах и ответах.


    До новых встреч!
    2007 При перепечатке, цитировании и другом использовании материалов ссылка на Сдай ЕГЭ и ЕНТ по математике на отлично! обязательна.
    Наверх
    В избранное