| ← Январь 2019 → | ||||||
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|---|---|---|---|---|---|---|
|
7
|
8
|
9
|
10
|
12
|
13
|
|
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
|
28
|
29
|
30
|
31
|
|||
За последние 60 дней ни разу не выходила
Сайт рассылки:
http://abakbot.ru
Открыта:
19-04-2013
Адрес
автора: comp.edu.abak-owner@subscribe.ru
Статистика
0 за неделю

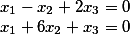
i%20+%20(%201%20)j%20+%20(%207%20)k)
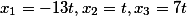
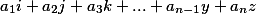
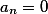 , а среди всех оставшихся есть хотя бы один не нулевой, то такая система решений не имеет
, а среди всех оставшихся есть хотя бы один не нулевой, то такая система решений не имеет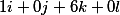
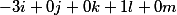
*x_{1}+(1)*x_{2}+(1)*x_{3}+(1)*x_{4}+(7)*x_{5}=0\\(5)*x_{1}+(1)*x_{2}+(1)*x_{3}+(7)*x_{4}+(7)*x_{5}+(-3)=0\\(8)*x_{1}+(7)*x_{2}+(6)*x_{3}+(5)*x_{5}=0\\)


%20=%20(-6.8266666666598E-11)*x^{3}+(256.00000000139)*x^{2}+(3743.9999999973)*x+(11663.999999981))
