Для общества нового типа необходима система оценки результатов выборов, когда голоса отдельных избирателей не имеют одинаковый вес. Ранжирование списка объектов оценщиками с неравными весами голосов, является частным случаем таких выборов.
Постановка задачи:
У нас есть N объектов, которые надо ранжировать и составить из них список от 1 до N, где номер 1 будет присвоен самому лучшему объекту, а номер N самому худшему объекту. Для проведения оценочной деятельности у нас есть L оценщиков, чьи голоса оцениваются не одинаково.
Необходимо разработать такой алгоритм подсчета голосов, чтобы оценка объектов была наиболее верной и была максимально защищена от действий по сговору отдельных групп оценщиков.
Линейный метод ранжированияДля этого каждый оценщик составляет свой список оцениваемых объектов, в котором располагает их в порядке убывания важности, присваивая самому лучшему объекту №1.
Далее каждому оцененному объекту присваивается оценочный балл Б = N – (порядковый номер в списке). Объект №1 будет иметь N-1 баллов, а объект с номером N будет иметь 0 баллов.
Поскольку, оценщики имеют разную величину голоса, учитываемого при оценке, то оценочные баллы должны быть умножены на коэффициент значимости оценщика (Кз). Для вычисления Кз конкретного оценщика, необходимо разделить количество принадлежащих ему голосов на сумму голосов всех оценщиков.
Далее нужно будет сложить полученные баллы для каждого оцениваемого объекта и получить окончательные оценочные баллы и список ранжирования по этим баллам.
Пример:
У нас есть три оценщика (А, В, С) с количествами голосов 25; 34; 41. И 10 оцениваемых объектов, для которых нужно составить ранжированный список и выбрать из них три лучших. Они составили три списка исходя из личных предпочтений. Определим коэффициенты значимости оценщиков.
Кз (А)= 25/(25+34+41)=0,25
Кз (В)= 34/(25+34+41)=0,34
Кз (С)= 41/(25+34+41)=0,41
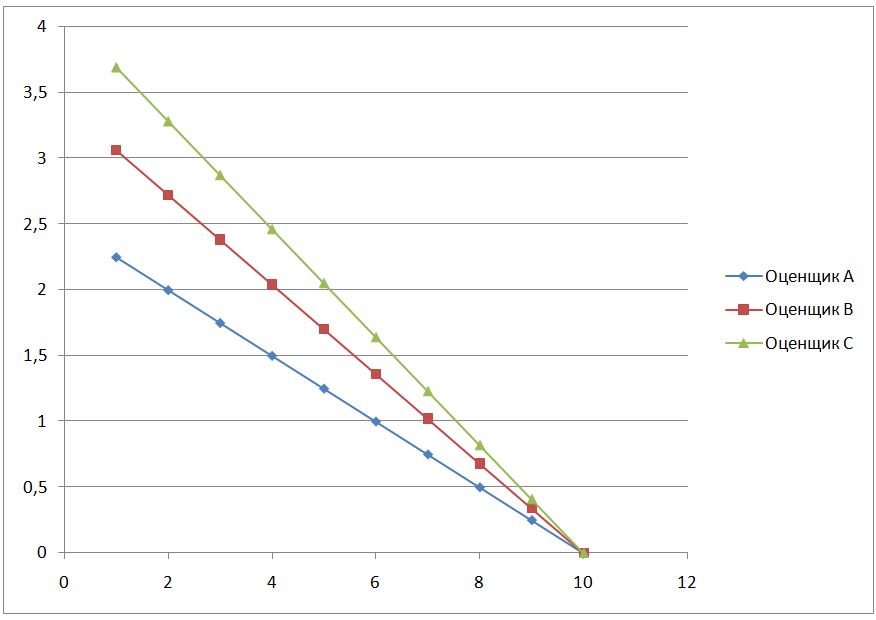
Применив полученные коэффициенты к спискам, получим три списка элементов с разными значениями важности. Эти списки можно представить на плоскости в виде прямых, где по оси Х порядковый номер объекта в списке, а по оси Y его значимость.
Суммировав оценки отдельно по каждому объекту, получим окончательный список ранжируемых объектов, где у наиболее значимого объекта будет наибольший суммарный балл. И окончательно выбрать три необходимые объекты с наибольшими суммарными баллами.
Недостатки метода:
Большая трудоемкость при достаточно большом количестве объектов, когда обычно стоит задача выбрать небольшое количество лучших
Возможность манипулирования по сговору. Часть оценщиков могут намеренно поставить какой-либо объект в конец списка, и он гарантированно не попадет в «призеры»
Для частичного устранения этих недостатков линейный метод можно модифицировать, задав количество значимых элементов в оцениваемом списке.
Для этого, каждый оценщик выбирает из предложенного списка R лучших, по его мнению объектов, и составляет ранжированный список из R элементов, присваивая самому лучшему объекту №1.
Далее каждому оцененному объекту присваивается оценочный балл Б = N – (порядковый номер в списке). Где N количество всех оцениваемых объектов. Объект №1 будет иметь N-1 баллов, а объект с номером R будет иметь (N – R) баллов. Остальным оцениваемым объектам, не попавшим в список лучших, присваивается (N – R - 1) баллов. В результате получаем список, где первые R элементов имеют убывающие баллы, а все последующие равны между собой. Затем, баллы в списке умножаем на коэффициент значимости оценщика (Кз). Имея ранжированные таким образом списки от всех оценщиков, суммируем полученные баллы для каждого оцениваемого объекта, и получаем окончательные оценочные баллы и список ранжирования по этим баллам.
Списки отдельных оценщиков можно представить на плоскости в виде ломанных прямых, где по оси Х порядковый номер объекта в списке, а по оси Y его значимость.
На рисунке представлен пример для трех оценщиков, где N=25 ; R=10
В данном случае трудоемкость процесса снижается, поскольку надо выбрать 10 лучших объектов и составить ранжированный список из них. Также, уменьшается возможность манипуляции путем предварительного сговора, поскольку нельзя будет сильно занизить значимость заранее обозначенных для этого объектов.
Линейный центрированный метод ранжирования
Можно применять, когда нужно ранжировать все объекты из списка
Так же как при линейном методе , каждый оценщик составляет свой список оцениваемых объектов, в котором располагает их в порядке убывания важности, присваивая самому лучшему объекту №1.
Далее каждому оцененному объекту присваивается оценочный балл Б = N – (порядковый номер в списке). Объект №1 будет иметь N-1 баллов, а объект с номером N будет иметь 0 баллов.
Оценочные баллы умножим на коэффициент значимости оценщика (Кз). Получим результаты, как в простом линейном методе.
Затем найдем центр, относительно которого будут рассматриваться полученные оценки. Для этого найдем центральную условную точку в оценках самого влиятельного оценщика.
Значение центральной точи Цт1= N/2*(Кз1) , где N – количество ранжируемых объектов, (Кз1) – коэффициент значимости самого влиятельного оценщика.
Теперь нам необходимо сделать так, чтобы оценки всех других оценщиков центральными точками совпали с этой точкой и при этом линии оценки не поменяли свои наклоны. Для этого оценки всех остальных оценщиков надо поднять на разницу их центральных точек
Центральная точка второго по значимости оценщика Цт2= N/2*(Кз2) ;
Цт1-Цт2= N/2*((Кз1)-(Кз2)) ; От сюда для второго оценщика набор данных будет следующим
(Оценка одного элемента оценщиком №2) = Б* (Кз2)+ N/2*((Кз1)-(Кз2)).
Аналогично можем найти значения данных для других оценщиков.
Получив оценочные баллы для каждого объекта от всех оценщиков, нужно сложить полученные баллы для каждого оцениваемого объекта и получить окончательные оценочные баллы и список ранжирования по этим баллам.
Пример:
У нас есть три оценщика (А, В, С) с количествами голосов 25; 34; 41. И 20 оцениваемых объектов, для которых нужно составить ранжированный список. Они составили три списка исходя из личных предпочтений. Определим коэффициенты значимости оценщиков.
Кз (А)= 25/(25+34+41)=0,25
Кз (В)= 34/(25+34+41)=0,34
Кз (С)= 41/(25+34+41)=0,41
Найдем разницу центральных точек
(СА) =20/2*(0,41-0,25)=1,6
(СВ)=20/2*(0,41-0,34)=0,7
Для списка оценщика (С) балы будут равны = Б* (Кз1) =Б*0,41
Для списка оценщика (А) балы будут равны = Б* (Кз3)+(СА) =Б*0,25+1,6
Для списка оценщика (В) балы будут равны = Б* (Кз2)+(СВ) =Б*0,34+0,7
Полученные данные можно представить на плоскости в виде прямых, где по оси Х порядковый номер объекта в списке, а по оси Y его значимость.
В данном случае, объекты оцениваются относительно центра выборки. И оценщики с меньшим весом оказывают меньшее влияние на ранжирование объектов относительно центра.
Центрированная ломанная оценкаЕсли нет необходимости ранжировать весь список, а только выбрать какое-то количество лучших элементов, то оценщики могут ранжировать в своих списках объекты выше центральной точки, остальным будет присвоено значение центральной точки.
Так же, при большом количестве оцениваемых объектов «центральную точку» можно сдвинуть (задав другой условный центр) чтобы уменьшить число ранжируемых объектов.
Нелинейный метод ранжированияТак же как при линейном методе , каждый оценщик составляет свой список оцениваемых объектов, в котором располагает их в порядке убывания важности, присваивая самому лучшему объекту №1. Введем переменную Р=(порядковый номер в списке)
Далее каждому оцененному объекту присваивается оценочный балл
Б = 1/КОРЕНЬ(Р)
Оценочные баллы умножаем на коэффициент значимости оценщика (Кз). Для вычисления Кз конкретного оценщика, необходимо разделить количество принадлежащих ему голосов на сумму голосов всех оценщиков.
Далее нужно будет сложить полученные баллы для каждого оцениваемого объекта и получить окончательные оценочные баллы и список ранжирования по этим баллам.
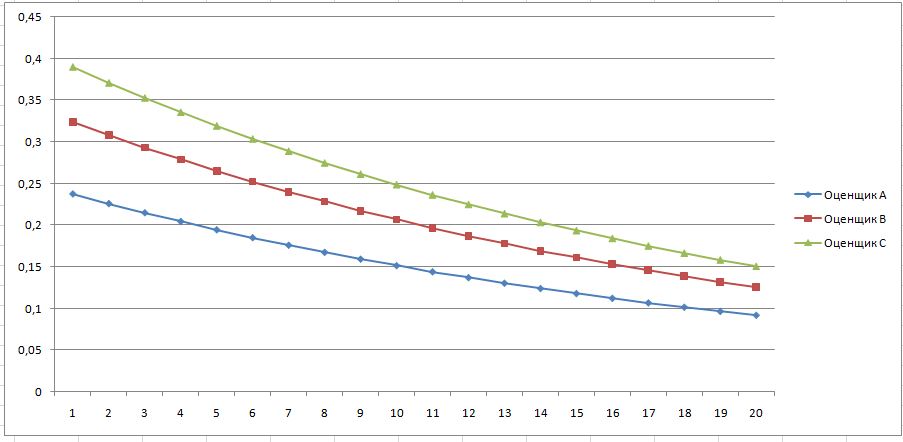
Списки отдельных оценщиков можно представить на плоскости в виде кривых, где по оси Х порядковый номер объекта в списке, а по оси Y его значимость.
Такой способ ранжирования можно применять при небольшом количестве ранжируемых объектов. Большое количество объектов сильно увеличит работу оценщиков, но не будет иметь практического значения.
Экспоненциальный метод ранжированияТак же как при линейном методе , каждый оценщик составляет свой список оцениваемых объектов, в котором располагает их в порядке убывания важности, присваивая самому лучшему объекту №1. Введем переменную Р=(порядковый номер в списке)
Далее каждому оцененному объекту присваивается оценочный балл
Б = ЕХР(-1*Р/М), где М коэффициент с помощью которого можно изменять кривизну оценочных кривых.
Оценочные баллы умножаем на коэффициент значимости оценщика (Кз). Для вычисления Кз конкретного оценщика, необходимо разделить количество принадлежащих ему голосов на сумму голосов всех оценщиков.
Далее нужно будет сложить полученные баллы для каждого оцениваемого объекта и получить окончательные оценочные баллы и список ранжирования по этим баллам.
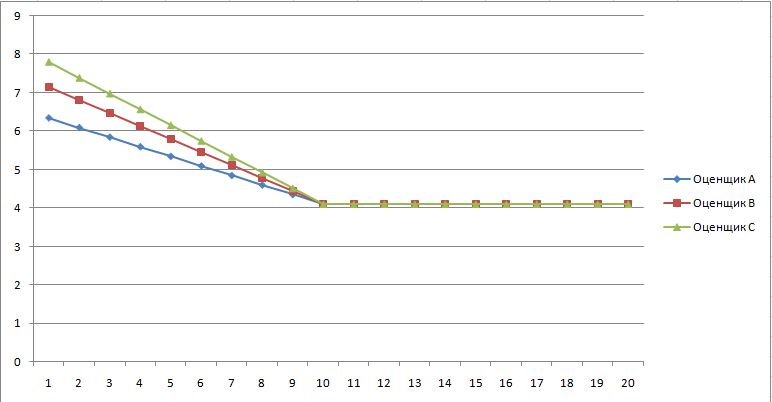
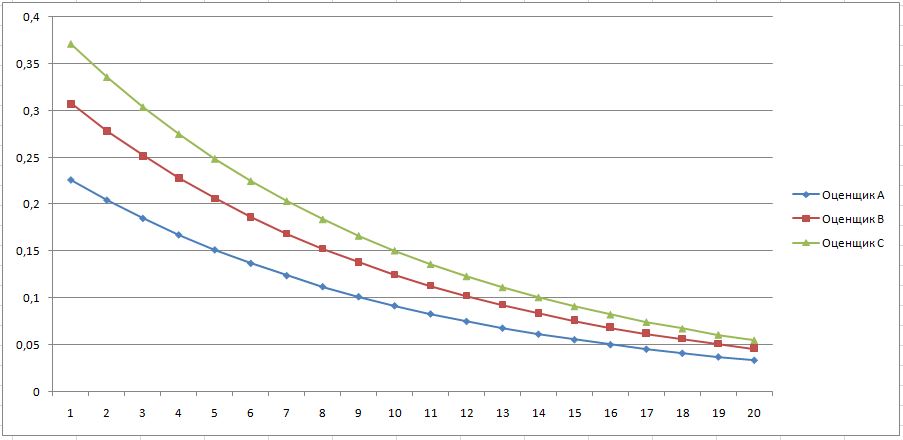
Списки отдельных оценщиков можно представить на плоскости в виде кривых, где по оси Х порядковый номер объекта в списке, а по оси Y его значимость.
М=10
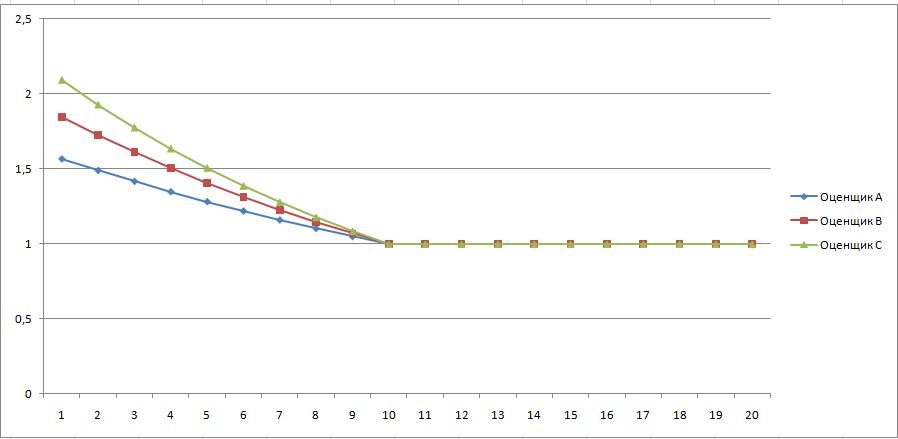
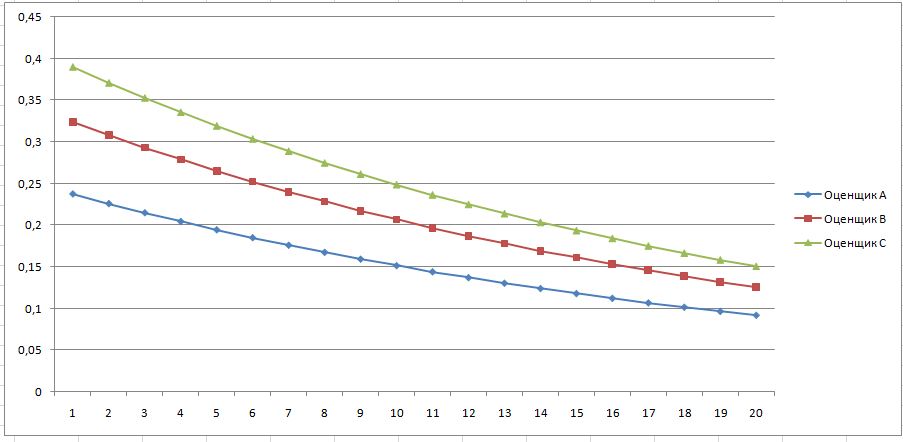
М=20
Экспоненциальный метод ранжирования удобен для подстройки под разное количество объектов с помощью коэффициента М.
Если нет необходимости ранжировать весь список, а только выбрать какое-то количество лучших элементов, то оценщики могут ранжировать в своих списках объекты выше заданной точки, остальным будет присвоено значение последней оцениваемой точки. В результате получи экспоненциальные кривые, переходящие в горизонтальные линии.
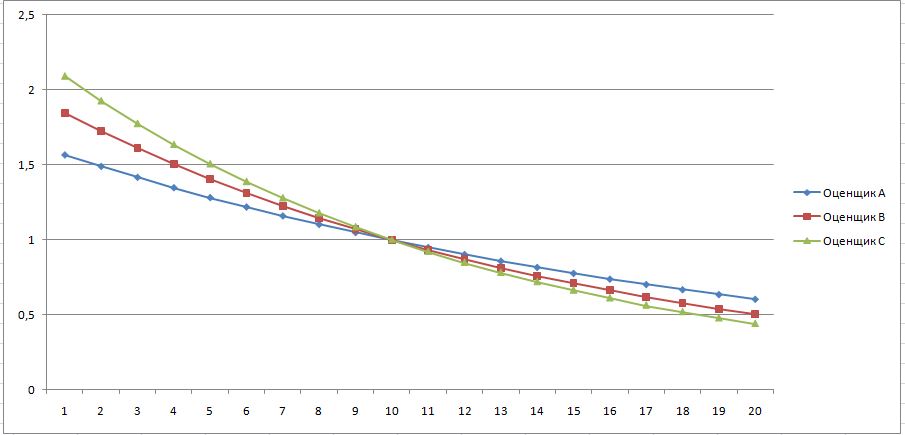
Экспоненциальный центрированный метод ранжированияЭтот метод похож на линейный центрированный, но только вместо линий используются экспоненциальные кривые, пересекающиеся в одной точке. Точка пересечения не обязательно будет в центре выборки. Ее положение определяется переменной задающей смещение.
Формула для расчета оценочных баллов выглядит следующим образом:
Б = ЕХР(-1*(Р-S)/М*Кз), где
Р- порядковый номер в списке
М - коэффициент, с помощью которого можно изменять кривизну оценочных кривых.
S – смещение от начала списка, где пересекаются оценочные кривые
Кз - коэффициент значимости оценщика
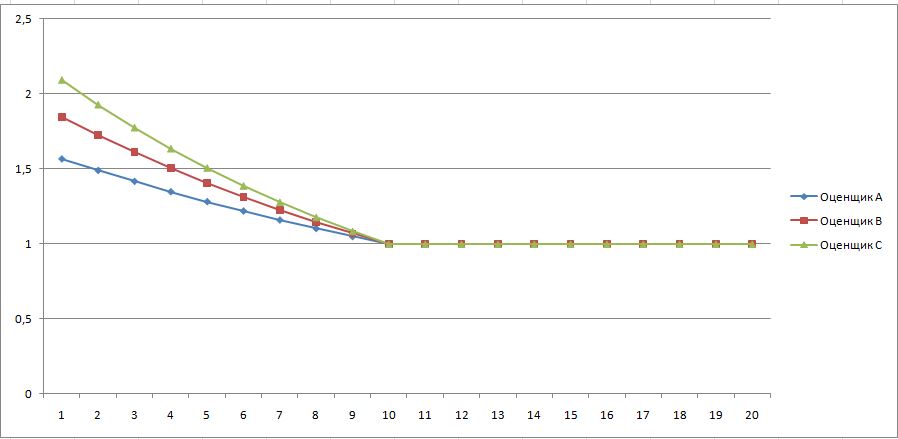
Если нет необходимости ранжировать весь список, а только выбрать какое-то количество лучших элементов, то оценщики могут ранжировать в своих списках объекты выше центральной точки, остальным будет присвоено значение центральной точки.
Экспоненциальный центрированный метод ранжирования является самым гибким и настраиваемым под разные текущие задачи.
Вступите в группу, и вы сможете просматривать изображения в полном размере

Это интересно
0
|
|||




Последние откомментированные темы:
-
Развитие ради развития
(1)
Meiskalt7
,
16.01.2022
-
Защита от социально-маркетинговой манипуляции
(1)
AlexFZF
,
29.05.2021
20250309172351