Идея о том, что силы, частицы и взаимодействия, которые мы видим сегодня, являются проявлениями единой всеобъемлющей теории, является привлекательной, требующей дополнительных измерений и множества новых частиц и взаимодействий. Многие такие математические конструкции существуют, чтобы исследовать, но без физической Вселенной, чтобы сравнить ее, мы вряд ли узнаем что-нибудь значимое о нашей Вселенной. (WIKIMEDIA COMMONS USER ROGILBERT) Нет, Вселенная Не Является Чисто Математической По Своей Природе Математика-это самый полезный инструмент, который мы имеем для понимания Вселенной. Но сам по себе он ни на что не отвечает.

На границах теоретической физики многие из наиболее популярных идей имеют одну общую черту: они начинаются с математической структуры, которая стремится объяснить больше вещей, чем наши преобладающие в настоящее время теории. Наши нынешние рамки для Общей Теории Относительности и квантовой теории поля отлично подходят для того, что они делают, но они не делают все. Они фундаментально несовместимы друг с другом и не могут достаточно объяснить темную материю, темную энергию или причину, по которой наша Вселенная наполнена материей, а не антиматерией, среди других загадок.

Это правда, что математика позволяет нам количественно описать Вселенную, это невероятно полезный инструмент, когда он применяется должным образом. Но Вселенная-это физическая, а не математическая сущность, и между ними есть большая разница. Вот почему одной математики всегда будет недостаточно, чтобы достичь фундаментальной теории всего.

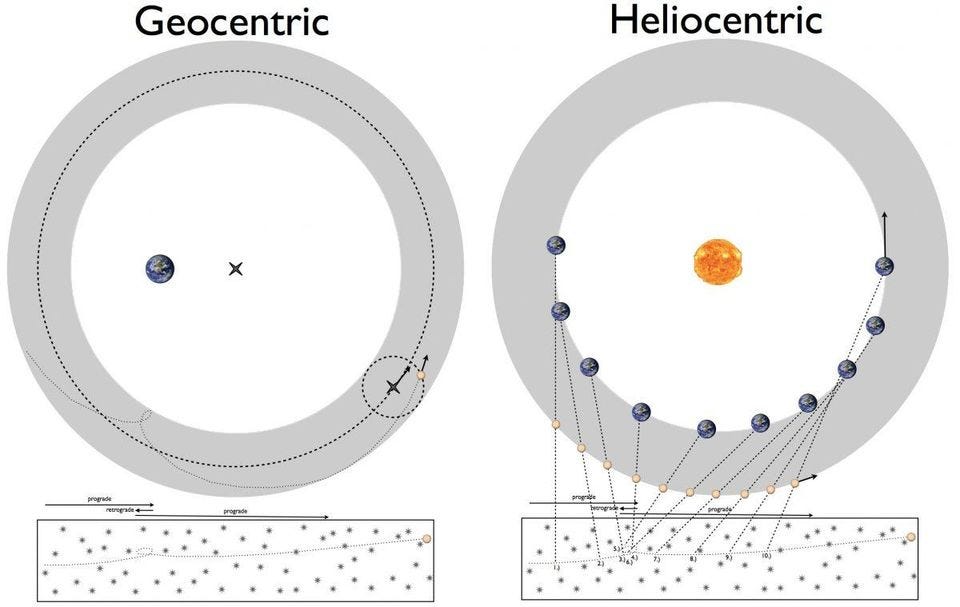
Одной из величайших загадок 1500-х годов было то, как планеты двигались в явно ретроградной манере. Это можно было бы объяснить либо с помощью геоцентрической модели Птолемея (L), либо с помощью гелиоцентрической модели Коперника (R). Однако доведение деталей до произвольной точности потребовало бы теоретических достижений в понимании правил, лежащих в основе наблюдаемых явлений, что привело к появлению законов Кеплера и, в конечном счете, теории всемирного тяготения Ньютона. (ИТАН СИГЕЛ / ЗА ПРЕДЕЛАМИ ГАЛАКТИКИ)

Около 400 лет назад развернулась битва о природе Вселенной. На протяжении тысячелетий астрономы точно описывали орбиты планет, используя геоцентрическую модель, в которой Земля была неподвижной, а все остальные объекты вращались вокруг нее. Вооруженный математикой геометрии и точными астрономическими наблюдениями — включая такие инструменты, как круги, экванты, деференты и эпициклы — точное математическое описание орбит небесных тел соответствовало тому, что мы видели эффектно.

Однако это совпадение не было совершенным, и попытки улучшить его либо привели к увеличению эпициклов, либо в XVI веке к гелиоцентризму Коперника. При размещении Солнца в центре, объяснения ретроградного движения стали проще, но соответствие данным было хуже. Когда появился Иоганн Кеплер, у него была блестящая идея, которая стремилась решить все проблемы.

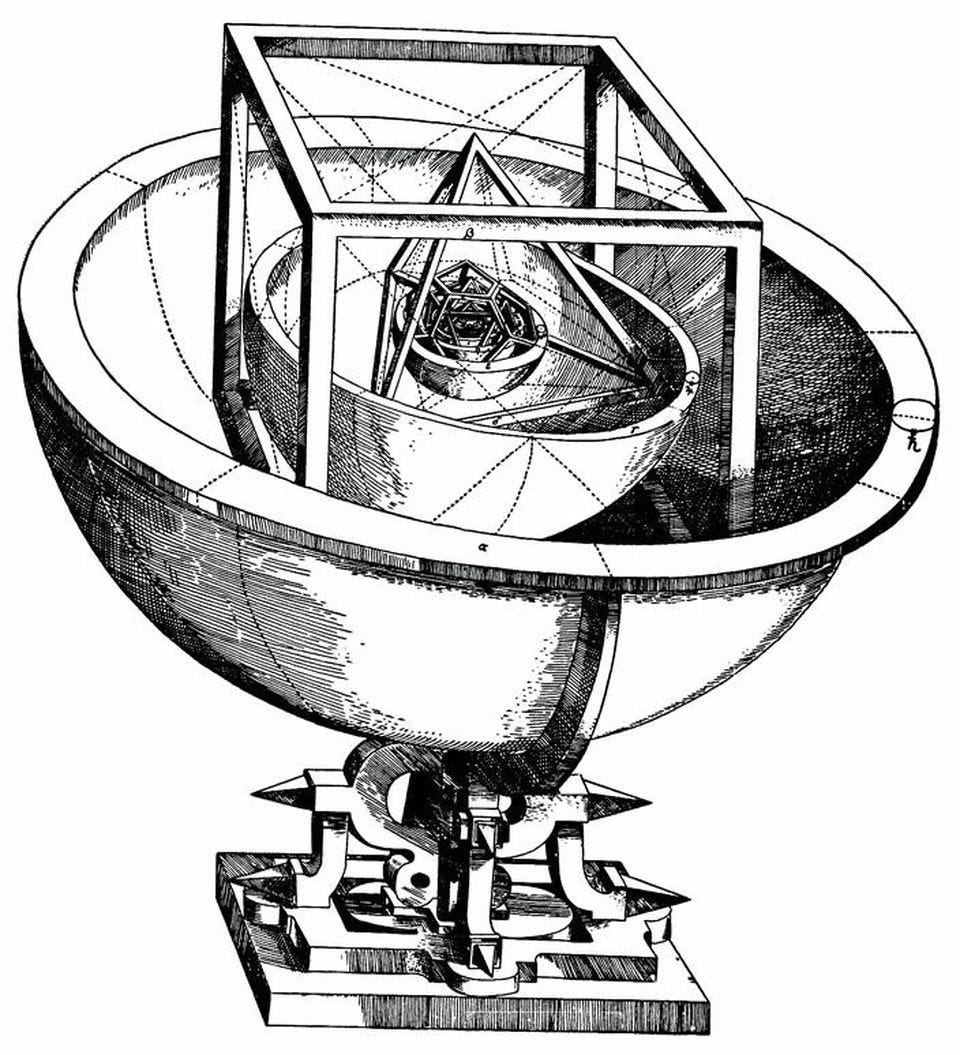
Имея каждую планетную орбиту на сфере, которая поддерживалась одним (или двумя) из пяти Платоновых тел, Кеплер теоретизировал, что должно быть ровно шесть планет с точно определенными орбитами. (J. KEPLER, MYSTERIUM COSMOGRAPHICUM (1596))

Он заметил, что всего было шесть планет, если считать Землю, но не Луну Земли. Он также заметил, что с математической точки зрения существует только пять Платоновых тел: пять математических объектов, грани которых являются равными многоугольниками. Рисуя сферы внутри и снаружи каждой из них, он мог бы “гнездить” их таким образом, чтобы они идеально подходили планетарным орбитам: лучше, чем все, что делал Коперник. Это была блестящая, красивая математическая модель, и, возможно, первая попытка построить то, что мы сегодня могли бы назвать “элегантной Вселенной”.

Но наблюдательно это не получилось. Она даже не была столь хороша, как древняя модель Птолемея с ее эпициклами, эквантами и деферентами. Это была блестящая идея, и первая попытка доказать — только из чистой математики — как должна быть устроена Вселенная. Но это просто не сработало.

То, что произошло дальше, было гениальным ходом, который определил наследие Кеплера.

Три закона Кеплера, что планеты движутся по эллипсам с Солнцем в одном фокусе, что они выметают равные площади За равные промежутки времени и что квадрат их периодов пропорционален кубу их полумягких осей, точно так же применимы к любой гравитационной системе, как и к нашей собственной Солнечной системе. (RJHALL / PAINT SHOP PRO)

Он взял свою красивую, элегантную, убедительную модель, которая не соответствовала наблюдениям, и выбросил ее. Вместо этого он пошел и углубился в данные, чтобы найти, какие типы орбит будут соответствовать тому, как на самом деле двигались планеты, и пришел к ряду научных (не математических) выводов.

1. Планеты двигались не по кругу вокруг Центрального Солнца, а скорее по эллипсам с Солнцем в одном фокусе, с различным набором параметров, описывающих эллипс каждой планеты.
2. Планеты двигались не с постоянной скоростью, а скорее со скоростью, изменяющейся в зависимости от расстояния планеты от Солнца, таким образом, что планеты охватывали равные площади в равное время.
3. И, наконец, планеты демонстрировали орбитальные периоды, которые были прямо пропорциональны длинной оси (главной оси) эллипса каждой планеты, поднятой до определенной степени (определяемой как 3/2).

Существует четыре известных экзопланеты, вращающихся вокруг звезды HR 8799, все из которых более массивны, чем планета Юпитер. Все эти планеты были обнаружены с помощью прямого изображения, сделанного в течение семи лет, и подчиняются тем же законам движения планет, что и планеты в нашей Солнечной системе: законам Кеплера. (JASON WANG / CHRISTIAN MAROIS)

Это был революционный момент в истории науки. Математика не лежала в основе физических законов, управляющих природой; она была инструментом, описывающим, как физические законы природы проявляют себя. Ключевым достижением, которое произошло, является то, что наука должна была основываться на наблюдаемых и измеримых вещах, и что любая теория должна была противостоять самим себе с этими понятиями. Без этого прогресс был бы невозможен.

Эта идея возникала снова и снова на протяжении всей истории, поскольку новые математические изобретения и открытия давали нам новые инструменты для описания физических систем. Но каждый раз новая математика не просто объясняла нам, как устроена Вселенная. Вместо этого новые наблюдения показали нам, что требуется нечто выходящее за рамки нашей нынешней физики, и одной только чистой математики было недостаточно, чтобы привести нас туда.

Мы часто визуализируем пространство как трехмерную сетку, даже если это зависящее от фрейма чрезмерное упрощение, когда мы рассматриваем концепцию пространства-времени. В действительности пространство-время искривляется присутствием материи и энергии, и расстояния не фиксированы, а скорее могут эволюционировать по мере расширения или сжатия Вселенной. (REUNMEDIA / STORYBLOCKS)

К началу 1900-х годов стало ясно, что ньютоновская механика находится в затруднительном положении. Она не могла объяснить, как объекты движутся со скоростью, близкой к скорости света, что привело к специальной теории относительности Эйнштейна. Теория всемирного тяготения Ньютона находилась в такой же горячей воде, так как она не могла объяснить движение Меркурия вокруг Солнца. Такие понятия, как пространство-время, только формулировались, но идея неевклидовой геометрии (где само пространство может быть искривленным, а не плоским, как трехмерная сетка) десятилетиями витала среди математиков.

К сожалению, разработка математической структуры для описания пространства-времени (и гравитации) требовала не только чистой математики, но и применения математики особым, тонким способом, который согласовывался бы с наблюдениями за Вселенной. Именно поэтому мы все знаем имя "Альберт Эйнштейн“, но очень немногие знают имя "Дэвид Гильберт".

Вместо пустой, пустой, трехмерной сетки, откладывание массы вниз вызывает то, что было бы "прямыми" линиями, чтобы вместо этого стать изогнутыми на определенную величину. Искривление пространства из-за гравитационных эффектов Земли является одной из визуализаций гравитационной потенциальной энергии, которая может быть огромной для таких массивных и компактных систем, как наша планета. (КРИСТОФЕР ВИТАЛЕ ИЗ NETWORKOLOGIES И ИНСТИТУТА ПРАТТА)

У обоих ученых были свои теории, связывающие искривление пространства-времени с гравитацией и присутствием материи и энергии . Оба они имели сходные математические формализмы; сегодня важное уравнение в Общей Теории Относительности известно как действие Эйнштейна-Гильберта. Но Гильберт, который придумал свою собственную, независимую от Эйнштейна теорию гравитации, преследовал более амбициозные цели, чем Эйнштейн: его теория применима как к материи и электромагнетизму, так и к гравитации.

И это просто не соответствовало природе. Гильберт строил математическую теорию так, как, по его мнению, она должна была быть применима к природе, и никогда не мог получить успешных уравнений, которые предсказывали количественные эффекты гравитации. Это сделал Эйнштейн, и именно поэтому уравнения поля известны как уравнения поля Эйнштейна, без упоминания о Гильберте. Без конфронтации с реальностью у нас вообще нет физики.

Электроны проявляют волновые свойства, а также свойства частиц, и могут быть использованы для построения изображений или зондирования размеров частиц так же, как свет может. Здесь вы можете увидеть результаты эксперимента, в котором электроны выстреливаются по одному через двойную щель. Как только достаточное количество электронов выстреливается, интерференционная картина может быть ясно видна. (THIERRY DUGNOLLE / ОБЩЕСТВЕННОЕ ДОСТОЯНИЕ)

Эта почти идентичная ситуация вновь возникла всего через несколько лет в контексте квантовой физики. Вы не можете просто запустить электрон через двойную щель и знать, основываясь на всех начальных условиях, где он окажется. Требовался новый тип математики-основанный на волновой механике и наборе вероятностных результатов. Сегодня мы используем математику векторных пространств и операторов, а студенты-физики слышат термин, который может зазвенеть колокольчиком: гильбертово пространство .

Тот же математик, Дэвид Гильберт, открыл набор математических векторных пространств, которые были чрезвычайно перспективны для квантовой физики. Только, опять же, его предсказания не совсем имели смысл, когда сталкивались с физической реальностью. Для этого необходимо было внести некоторые изменения в математику, создав то, что некоторые называют сфальсифицированным гильбертовым пространством или физическим гильбертовым пространством. Математические правила должны быть применены с определенными конкретными оговорками, иначе результаты нашей физической Вселенной никогда не будут восстановимы.

Картина слабого изоспина, T3 и слабого гиперзаряда, Y_W и цветового заряда всех известных элементарных частиц, повернутых на слабый угол смешивания, чтобы показать электрический заряд, Q, примерно по вертикали. Нейтральное поле Хиггса (серый квадрат) нарушает электрослабую симметрию и взаимодействует с другими частицами, чтобы придать им массу. Эта диаграмма показывает структуру частиц, но имеет корни как в математике, так и в физике. (CJEAN42 ВИКИМЕДИА КОММОНС)

Сегодня в теоретической физике стало очень модно обращаться к математике как к потенциальному пути к еще более фундаментальной теории реальности. На протяжении многих лет был опробован ряд математических подходов:

• наложение дополнительных симметрий,
• добавление дополнительных измерений,
• добавление новых полей в Общую Теорию Относительности,
• добавление новых полей в квантовую теорию,
• использование больших групп (из математической теории групп) для расширения Стандартной модели,

вместе со многими другими. Эти математические исследования интересны и потенциально релевантны для физики: они могут содержать подсказки о том, какие секреты Вселенная может иметь в запасе за пределами того, что известно в настоящее время. Но математика сама по себе не может научить нас, как устроена Вселенная. Мы не получим никаких окончательных ответов, не сопоставив его предсказания с самой физической Вселенной.

Визуализация умножения единичных октонионов, которых насчитывается 8, требует мышления в многомерных пространствах (слева). Таблица умножения для любых двух единичных октонионов также показана (справа). Октонионы-это увлекательная математическая структура, но она предлагает неидеальные решения для множества возможных применений. (YANNICK HERFRAY (L), АНГЛИЙСКАЯ ВИКИПЕДИЯ (R))

В некотором смысле, это урок, который каждый студент-физик изучает в первый раз, когда они вычисляют траекторию объекта, брошенного в воздух. Как далеко это может зайти? Где же он приземляется? Сколько времени он проводит в воздухе? Когда вы решаете математические уравнения-уравнения движения Ньютона-которые управляют этими объектами, вы не получаете “ответ.” Ты получишь два ответа, вот что дает тебе математика.

Но на самом деле, есть только один объект. Он следует только по одной траектории, приземляясь в одном месте в одно определенное время. Какой ответ соответствует действительности? Математика вам этого не скажет. Для этого вам нужно понять особенности рассматриваемой физической проблемы, так как только это скажет вам, какой ответ имеет физический смысл за ним. Математика поможет вам очень далеко продвинуться в этом мире, но она не даст вам всего. Без конфронтации с реальностью вы не можете надеяться понять физическую вселенную.

https://medium.com/starts-with-a-bang/no-the-universe-is-not-purely-mathematical-in-nature-d202e2d7f03e