В клубе появилась целая серия статей, список которых приведен в конце статьи, и в которых утверждается фрактальная структура мироздания. Насколько это так?
Прежде всего, что такое фрактал?
Согласно Википедии, фрактал есть некий объект, части которого совпадают с ним самим – точно или приближенно, самоподобный объект. Причем, это совпадение вовсе не обязательно должно быть наглядным геометрически.
Фрактал:
––1. Должен иметь сложную структуру, чтобы обнаруживать свою топологию при любом увеличении;
––2. Является самоподобным:
––3. Может быть построен рекурсивными процедурами.
Фрактал должен обязательно обладать первым свойством и то ли вторым, то ли третьим, или же всеми тремя.
Это может быть, например, геометрический объект, простейшим случаем которого является бинарное дерево:
Рис. 1. Бинарное дерево.
Этот объект построен из двоичной пары – двух веточек, и обнаруживает свое самоподобие при любой степени увеличения. Для построения такого фрактала требуется бесконечное количество итераций, на каждой из которых размер исходной пары уменьшается в определенное число раз. Чертеж естественно не может демонстрировать бесконечное число – на нем принято ограничение восемью уровнями.
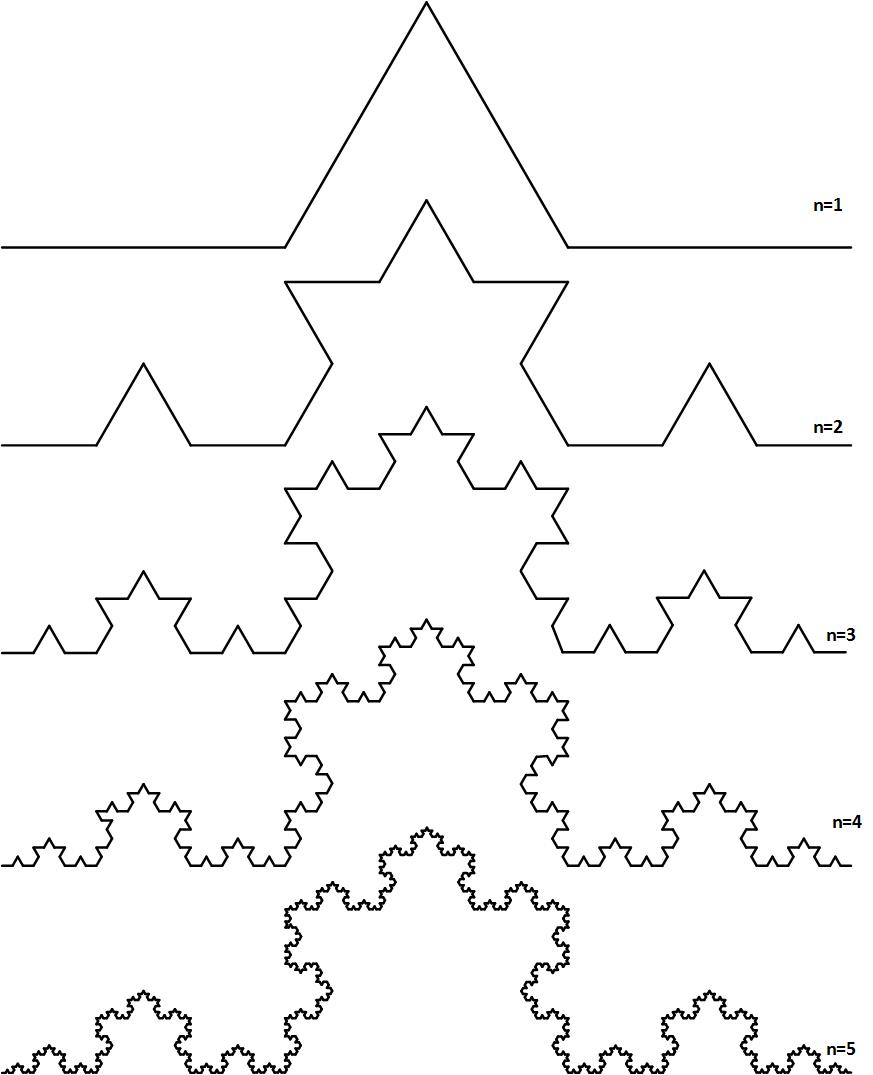
Другой интересный пример – кривая Коха:
Рис. 2. Кривая Коха.
На уровне n=1 фигура состоит из четырех отрезков. На каждом следующем уровне n каждый из отрезков заменяется исходной фигурой с уровня n-1. Повторяя итерации бесконечное число раз, в пределе при n → ∞ получится хитрая кривая, к которой ни в одной точке нельзя провести касательную, то есть, в каждой точке она не имеет производной. Любая степень увеличения покажет на любом уровне наличие базовой конфигурации, что и является самоподобием.
Однако, самоподобие может быть не только геометрическим, визуальным. Один из известнейших примеров – множество Мандельброта (рис. 3).
Рис. 3. Множество Мандельброта.
Принцип его построения – алгебраические итерации на плоскости комплексных чисел. Известно, что комплексное число Z=x+iy можно представить точкой с координатами {x,y} в плоской декартовой системе координат. Множество Мандельброта – множество комплексных чисел, каждое из которых Zn образуется из предыдущего Zn-1 рекурсивно по закону:
где константа C – тоже комплексное число. Конкретный вид множества определяется парой комплексных чисел Z0=x0+iy0 и C=a+ib. На первый взгляд в картинке мало «фрактального». Однако, множество точек на ней очерчено очень сложной структурой. Хорошо видно самую крупную кривую – кардиоиду. Все овалы, которые ее касаются, при большом увеличении показывают тоже сложную структуру, что видно из фрагмента границы множества на рис. 4.
Рис. 4. Фрагмент границы множества Мандельброта при большом увеличении.
На каждом овале виден меньший овал, на вершине которого имеется какой-то «нарост». Если увеличивать фрагменты изображения, то оказывается, что этот «нарост» повторяет исходный овал со своим таким же «наростом», который тоже повторяет предыдущий – и так далее. Существуют множество программ для построения этого фрактала. Для эффектности элементы множества, а чаще точки за его пределами закрашиваются каким-либо алгоритмом. Можно даже найти онлайн-программы для такого построения, например, ЗДЕСЬ.
При проведении параллелей между реальной природой и математическими фракталами сразу нужно сказать, что в природе ни сколько-нибудь точного самоподобия, ни большого количества уровней самоподобия не существует. Поэтому природную, натуральную фрактальность, там, где она имеет место, следует называть квазифрактальностью. Таким квазифракталом можно считать, например, структуру прожилок кленового листа (рис. 5).
Рис. 5. Прожилки на кленовом листе.
Бинарное дерево – один из самых распространенных квазифракталов в природе. Это – и лист на рис. 5, и структура ветвей дерева, структура кровеносных сосудов и нервных волокон человека, и другие.
Однако, зачастую фракталом называют просто какие-то сложные структуры из природы. Например, изображение фрагмента береговой линии озера Ататюрка, полученное космическими съемками (рис.6):
Рис. 6. Фрагмент береговой линии озера Ататюрка в Турции.
На первый взгляд эта очень живописная линия чем-то напоминает границу множества Мандельброта на рис. 4. Однако, при трезвом размышлении следует сделать вывод, что эта линия наверняка не может быть построена пусть не алгебраической, пусть какой-то простой логической рекурсией. Более того, внимательное рассмотрение показывает полное отсутствие самоподобия, все извилины берега совершенно случайны, поэтому ни о какой фрактальности здесь речи быть не может.
Зачастую очертания берегов объявляют природным фракталом при сравнении с кривой Коха (рис. 2), которую можно считать похожей на берег какого-то фантастического водоема. Однако, любые очертания берегов имеют сугубо случайную извилистость. Случайность – главный враг «фрактальности», принципиально периодической структуры, для которой необходимо еще и самоподобие хотя бы на трех – четырех уровнях.
Вернемся теперь к фрактальности Вселенной. В указанных статьях в качестве доказательства фрактальности Вселенной приводится известный снимок, сделанный телескопом «Хаббл» (рис.7):
Рис. 7. «Волокнистая» структура Вселенной.
Я думаю, что снимок говорит сам за себя. Форма, густота, конфигурация галактик и их скоплений, филаментов – «космических нитей» – совершенно случайны, без какого-либо намека на повторяемость, что говорит о том, что это – не фрактал, а совершенная его противоположность. И вообще, никакие топологические структуры не повторяются на уровнях планетная система – галактика – кластер – суперкластер. Вращение небесных тел и их ассоциаций вокруг какого-то центра нельзя считать признаком фрактальности, поскольку вращение является динамическим атрибутом, но никак не топологическим.
Поэтому я считаю высказывания типа «Вселенная – это фрактал» сделанными ради красного словца. Логика, которой авторы статей убеждают в этом, подобна логике Паниковского, когда Шура спросил его про гири: «А вдруг они не золотые?» он ответил: «А какие же они по-вашему?»
Более того, на основании «фрактальности Вселенной», которую ее апологеты считают доказанной (а какая же она по-вашему?), делаются далеко идущие выводы. Один из самых распространенных – фрактальность означает неоднородность, а значит решения Фридмана уравнений Эйнштейна, из которых Гамовым сделан вывод о Большом взрыве, неверны, Большого взрыва, следовательно, не было, расширения нет, и всю современную космологию – в мусорку. А там и ОТО, как основной аппарат космологии, и вообще, такой-сякой Эйнштейн отказался от эфира, чем вверг современную физику в статус мифа. Сколько песен в КЛК уже пелось под эту музыку!
Дело в том, что однородность и изотропность Вселенной, которые не признаются «альтернативщиками», друг без друга не существуют. Если Вселенная однородна, то она изотропна, если изотропна – то однородна. Если Вселенная обладает для нас одинаковыми свойствами в любом направлении, то она изотропна. Именно это и наблюдается, мы не можем сказать, например, что справа прилетает гораздо больше фотонов реликтового излучения, чем слева. Если выбрать к примеру телесный угол в 1 квадратный градус, то куда бы мы его не направили, в него попадет примерно одинаковое число наблюдаемых галактик. При этом совершенно все равно, имеет ли место квазифрактальность Вселенной, что делает тем более бессмысленными заявления о том, что она – фрактал. Свойства Вселенной одинаковы в любом направлении. Конечно, с определенной степенью точности, но все дело в том, что эта степень довольно высока. Безусловно, существуют суперкластеры галактик и супервойды, вносящие отклонения однородности распределения материи от идеальной. Но это отклонение измерено, отражением степени изотропности Вселенной является степень изотропности реликтового излучения, а она составляет порядка 0.001%. А это означает не что иное, что исходные предположения для решений Фридмана были сделаны совершенно адекватно.
Реликтовое излучение в этом контексте обладает уникальными свойствами. Почти точное совпадение его спектра со спектром излучения абсолютно черного тела означает, что в момент его образования излучающая среда находилась в состоянии термодинамического равновесия. А этот факт решающим образом подтверждает теорию горячей Вселенной Гамова, а значит и Большой взрыв. В то же время флуктуации от изотропности означают, что уже через 380 000 лет после Большого взрыва образовывались локальные неоднородности, которые и привели к образованию больших космических объектов.
Статьи в КЛК, о которых идет речь:
Вселенная оказалась фракталом
Почему время идёт только вперёд?
Фрактальная Вселенная — преграда космической экспансии
Фракталы в природе
Вступите в группу, и вы сможете просматривать изображения в полном размере

Это интересно
+1
|
|||









Последние откомментированные темы:
-
Ответы на детские вопросы про "Лунную Афёру"
(1)
kauperwud
,
28.02.2022
-
Космический корабль в несколько километров: все, что известно о новом проекте Китая
(2)
андрей1
,
27.02.2022
-
ЗАГАДКИ "ПАРАДОКСА ФЕРМИ" БОЛЬШЕ НЕТ?
(3)
donskarloss@gmail.com
,
27.02.2022
-
Марсианские реки
(1)
donskarloss@gmail.com
,
27.02.2022
-
Семь спорных причин считать, что на Земле существовали цивилизации до людей
(1)
donskarloss@gmail.com
,
24.02.2022
20250109082148