Когда наш неутомимый Вл.Дм. репостил статью акад. РАН С. Герштейна «О двух распространенных ошибках в понимании принципов ОТО и СТО», в своем комментарии к ней Л.М. Топтунова заявила: «Все (!) теоретики в физике идут не от природы к математике, а от математики к природе. Они получают красивые теории. Но беда в том, что математические теории строятся для идеализированных условий, которые в природе никогда не осуществляются». Поставлено клеймо сразу на всех теоретиков. Я хотел возразить на это комментарием, но понял, что для краткого комментария тема слишком широка. Особенно если учесть появление в том же авторстве статьи «Почему классическая математика так плохо работает на практике». Поэтому решил разразиться статьей.
В нашем клубе появляется все больше публикаций, противопоставляющих физику и математику. В основном считают, что физики «уходят с дороги», чрезмерно увлекаясь какими-то красивыми математическими теориями, в угоду этой красоте теряя физический смысл описываемой проблемы. Витают во облацех. Математика – наука абстрактная, физика же – наука конкретная, жизненная, поэтому математика уводит незадачливых физиков от физических реалий.
К сожалению, подобные взгляды широко распространены, и зачастую находят сочувствие. Это понятно, потому что далеко не все интересующиеся устройством мироздания обладают надлежащими познаниями в физике даже в рамках программы средней школы. Многие явления природы им кажутся «и так понятными», не требующими применения какой-то «заумной» математики. С математическими же познаниями дело обстоит еще хуже. Если знание математического анализа худо-бедно свойственно имеющим высшее техническое образование, то со знаниями в области, например, математической физики и тензорного исчисления наблюдается глубокий вакуум. Отсутствие необходимых познаний вообще порождает множество доморощенных специалистов, больше всего в медицине, экономике, и вот теперь в физике. Высказывания таких специалистов характеризуются прежде всего безапелляционностью, безосновательностью. Это тоже понятно.
Физика – это не полигон для демонстрации красивых абстрактных математических теорий, которые могут иметь, а могут и не иметь никакой связи с реальностью. Физика вынуждена использовать математику в чисто утилитарных целях, а именно как наилучший язык логических рассуждений, при использовании которого в минимальной степени допустимы неправильные следствия. Именно поэтому все физические законы выражаются математическими формулами, благодаря которым эти законы становятся строгими, не допускающими двояких толкований. Этим физические теории отличаются от псевдофизических, псевдонаучных. Говоря о таких «теориях», можно выделить несколько частных тенденций в их связи с математикой.
Первая – это вообще отказ от математики. За примером далеко ходить не нужно – это чудесатое сочинение В.М. Антонова «Эфир», опубликованное недавно в нашем клубе несколькими статьями. Это сочинение – пример того, что без использования математики можно болтать все, что угодно. И про «скользкие шарики» эфира, и про «пушистые электроны», и про размер этих шариков, который оказывается в 100 раз большим размера протона, который из этих шариков состоит, про «присасывающие жёлобы атомов» и прочую дурь. Чуть ли не в каждой строчке выдумываются какие-то утверждения, ниоткуда не следующие, которые никак нельзя проверить. Их даже опровергнуть нельзя, их столько, что, как говорят в народе, «заморишься» опровергать.
Вторая тенденция – безграмотное использование математики. Здесь яркий пример – работа А.В. Рыкова «Основы теории эфира». В ней набросано множество формул, зачастую взятых «ниоткуда», плохо связанных между собой, содержащих в себе явные ошибки, вызванные откровенным непрофессионализмом, причем, такие принципиальные ошибки лежат в самой основе его теории. Известным апологетом этой теории является Л.М. Топтунова, я уж и боюсь ей посоветовать проделать те элементарные математические выкладки, которые там приведены, чтобы убедиться в их безграмотности. Не хочу здесь приводить конкретный их анализ, это долго и вряд ли кто будет это читать, но при желании могу и показать это!
Третья тенденция – обратная. Среди «альтернативщиков» есть весьма грамотные и образованные люди, которые выдвинули какие-то свои теории, но для их доказательства за неимением фактов прибегают к «наукообразию». Пример такой тенденции – позабытая сейчас, но очень модная в 90-х годах теория торсионных полей. Я тогда даже книгу Шипова купил, глянул в нее при покупке – вроде как научная, с математикой, значит, наверное, серьезная. Хотелось изучить, интересно же – торсионные поля! Не получилось, книга перегружена, забита математическим формализмом, мне, физику-любителю даже с моим физфаковским образованием изучить это все оказалось не под силу. Поговорил с однокурсниками-теоретиками, подтвердили: «наукообразие» книги – способ маскировки бездоказательности, беспомощности выдвигаемой физической концепции. Посмеялись над моей наивностью. Я успокоился по поводу своих сомнений в собственной состоятельности.
Конечно, качество физической теории не может не зависеть от качества используемых математических средств. Поэтому физик должен быть не только физиком и философом, но еще и достаточно хорошим математиком. Эйнштейн потратил много времени и усилий, изучая риманову геометрию начиная с времен Гаусса, и включая исследования Леви-Чивита и Кристоффеля. Зная, что эта теория в то время для физиков была новой, в своих работах по ОТО он в начале излагал требуемые знания из этой геометрии.
Вообще всегда следует рассматривать две стороны физической теории. Во-первых, сама физическая модель. Ее основой является обычно ряд фундаментальных уравнений. Эти уравнения описывают физическую реальность, поэтому нельзя говорить, что теория «окажется полуэмпирической, т. е. будет построена на приблизительных зависимостях, найденных из опыта» (цитирую Л.М. Топтунову). Уравнения в теории описывают какие-то законы, поэтому они должны быть не точны, а правильны. Приведу в пример некоторые великие уравнения, которые никак нельзя охарактеризовать словами Людмилы Михайловны. Самый первый пример – безусловно основное уравнение классической механики, ньютоновское уравнение движения. В одномерном случае это:
Точкой здесь обозначена операция полной производной по времени. Само по себе это уравнение не может являться точным, неточным или приблизительным. Оно является правильным, потому что правильно описывает закон движения. Или волновое уравнение для электромагнитного поля:
Где А – векторный потенциал поля. Можно ли говорить о том, что оно точно или неточно? То же относится к уравнению Шредингера в квантовой механике и к уравнениям Эйнштейна в теории относительности. Эти великие уравнения записаны строгим, сухим, абстрактным математическим языком. Но идеализированы ли они? Оторваны ли они от действительности? Можно ли считать их «приблизительными»?
Дело в том, что с конкретной реальностью эти уравнения связывают их решения. Тут как раз и требуется устанавливать какие-то условия и делать какие-то оправданные допущения и приближения, исходя именно из физической реальности. Вот и выходит, что волновое уравнение есть совершенно адекватная реальности математическая модель электромагнитного поля. Потому что для расчета, скажем, антенны самолетного радара, или параметров сложной микрополосковой СВЧ-линии, требуются задания как минимум определенных краевых условий, которые сами по себе с одной стороны являются упрощениями, а с другой – той самой связью с конкретной реальностью. Причем именно такие условия определяют вид решений этих уравнений, кардинально различающихся для разных условий.
Далее в указанном комментарии следуют высказывания об ОТО: «при создании ОТО молчаливо предполагалось, что пространство имеет однородные и одинаковые во всех направлениях свойства на любых масштабах» – это не так, это заявление выдумано. Как раз об этом я только что говорил. Сама по себе ОТО – это физическая концепция, в первую очередь это – уравнения Эйнштейна. Если вы хотя бы чисто внешне познакомитесь с ОТО, то увидите, что для получения этих уравнений вовсе не требуются изотропность и однородность Вселенной – они справедливы и для неоднородной и для неизотропной Вселенной тоже. Уравнения Эйнштейна для гравитационного поля получаются из чисто физического, теоретико-механического принципа наименьшего действия, что показано, кстати, позже их появления Гильбертом и Лоренцем, об этом говорил сам Эйнштейн. Требования однородности и изотропности понадобились значительно позже А.А. Фридману для решения уравнений Эйнштейна в такой Вселенной, причем, без привлечения космологической постоянной. И уже на основе этих решений он пришел к выводу о нестационарности Вселенной.
Кстати, понятия однородности и изотропности вводятся для масштабов, гораздо больших, чем те, о которых говорится в указанном комментарии. То же относится и к фрактальности. Да и несколько похожие структуры материи для кластеров и для суперкластеров галактик не дают повода говорить о фрактальной структуре вообще, которая должна подразумевать по крайней мере несколько таких уровней.
То же можно сказать и о решении Шварцшильда для движения в центрально-симметричном гравитационном поле, которое кроме такой симметрии, подразумевает пустое пространство и строгую сферичность тяготеющей массы – при этих условиях решение Шварцшильда является точным, в том смысле, что оно является точным аналитическим решением системы дифференциальных уравнений, при получении которого не требуется приближенных методов.
В заключение о фразе из того же комментария: «с каждым новым наблюдением, астрофизикам приходится подгонять ОТО под реальность путём введения всё новых и новых гипотез». Как говорится, на совесть автора. Судя по публикациям, практически каждое крупное открытие в астрофизике подтверждает выводы ОТО, не требуя никаких «подгонок». Да и что это могут быть за подгонки? Вид уравнений Эйнштейна? Какие-то их решения? Эти подтверждения – соответствие теоретическим значениям потерь энергии на гравитационное излучение двойных нейтронных звезд, сама регистрация предсказанных теорией гравитационных волн, куча подтверждений, полученных при регистрации гравитационных волн от слияния нейтронных звезд. Сюда входит равенство скоростей распространения гравитации и света, строго доказанное вопреки заверениям о бесконечности скорости гравитации, строгое соответствие при этом формы, амплитуды и частоты чирпа теории, позволившее создать первый прямой метод определения межгалактических расстояний («стандартные сирены»). Это полное соответствие параметров первой фотографии черной дыры теории, это удивительное соответствие теории параметров реликтового излучения, это точные измерения галактического и звездного гравитационного линзирования и микролинзирования, … Этого что мало? Причем, это все далеко не мелочи. Это – крупные, хорошо исследованные и доказанные экспериментальные факты, а не очередные выдумки «антирелятивистов».
Выводы.
- Коллизии несоответствия математики и физики надуманы. Математический аппарат есть логика физики, неотъемлемая часть физической концепции.
- Случаи «ненормального» математического аппарата в теории или его отсутствие являются признаком псевдонаучности.
- Следует понимать различную роль и различные свойства уравнений и их решений в физике.
- Последние крупные открытия в астрофизике кроме своего основного значения являются убедительными подтверждениями общей теории относительности как основы астрофизики и космологии.
Вступите в группу, и вы сможете просматривать изображения в полном размере

Это интересно
+1
|
|||

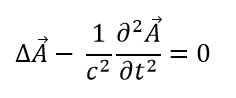


Последние откомментированные темы:
-
Ответы на детские вопросы про "Лунную Афёру"
(1)
kauperwud
,
28.02.2022
-
Космический корабль в несколько километров: все, что известно о новом проекте Китая
(2)
андрей1
,
27.02.2022
-
ЗАГАДКИ "ПАРАДОКСА ФЕРМИ" БОЛЬШЕ НЕТ?
(3)
donskarloss@gmail.com
,
27.02.2022
-
Марсианские реки
(1)
donskarloss@gmail.com
,
27.02.2022
-
Семь спорных причин считать, что на Земле существовали цивилизации до людей
(1)
donskarloss@gmail.com
,
24.02.2022
-
ОБРАЩЕНИЕ.
(4)
vladmiza
,
24.02.2022
-
Старт переносится на... Как часто нам это приходится слушать? Ну когда же, наконец!
(1)
тимм
,
23.02.2022
-
Выйдя в межзвездное пространство, «Вояджеры» стали передавать сигналы, которые сильно заинтересовали
(2)
тимм
,
23.02.2022
-
Гравитация, время, карусель
(1)
vladmiza
,
20.02.2022
-
НАСА надоели разговоры о смертоносной планете Нибиру, и оно выступило с заявлением
(8)
maestro1965
,
20.02.2022
20250307051116