Данная статья – ответ на статью Л.М. Топтуновой «Много ли нестыковок и ошибок в релятивистской теории?».
Уважаемая Людмила Михайловна, убедительно прошу вас все же прочесть эту статью, несмотря на то, что я «ортодокс», «репродуктор» и т.п., из-за чего вы мои опусы игнорируете.
«Нестыковок и просто ошибок много», утверждается в вашей статье. И далее следует ваша аргументация. Будем ее рассматривать по порядку.
Сначала насчет преобразований Лоренца у Эйнштейна, Паули и Борна. В своей предыдущей статье я на конкретных цитатах показал, что у указанных авторов, и еще у Ландау и у Левича вывод этих преобразований, вопреки измышлениям г-на Акимова, дает совершенно одинаковые результаты, и никаких противоречий нет, несмотря на то, что используются различные способы вывода. Кажущиеся противоречия по замедлению времени объясняются вашим поверхностным взглядом на формулу замедления времени. В самом деле, связь между промежутком времени Δt’, прошедшем по часам, покоящимся в движущейся системе отсчета, проще говоря, по часам в ракете, и этим же промежутком времени Δt , но измеренным по часам на Земле (смотрим, например, Ландау, у других – то же), задается формулой:
та же формула и у остальных источников. Это означает, что если, например, скорость V такова, что значение квадратного корня равно 1/3, то если на ракете прошло Δt’ = 1 год, то на земле за это время пройдет 3 года. То есть, постареет именно тот, кому надо постареть. Просто не нужно путать, где система подвижная, а где – неподвижная.
Теперь по поводу «диаграммы Минковского». Я не читал доклада Минковского, и не был 21 сентября 1908 года в Кельне. Скорее всего, это очередные измышления того же автора, который там тоже не был, и которого вы опять повторяете. Так вот, именно этим «геометрическим» методом выводятся преобразования Лоренца в курсе Ландау. Для этого используются известные теоретико-механические свойства вращения систем координат, одна из которых – временна́я. Переход от какой-то движущейся инерциальной системы отсчета к другой инерциальной можно описать поворотом их систем координат одной относительно другой на определенный угол, определяемый скоростью. Из-за того, что в классике инвариантом является длина отрезка dl2 = dx2 + dy2 + dz2, а в геометрии Минковского, аппарате СТО, значение интервала ds2 = c2dt2 – (dx2 + dy2 + dz2), преобразования при таком повороте в классике описываются через тригонометрические функции, а в СТО из-за знака «–» – через гиперболические. Это как раз и отражается на приводимой в вашей статье картинке – слева Эвклид, справа – Минковский, там – простая 2-мерная аналогия.
Так вот, используя тот же метод, что и Минковский, Ландау получает преобразования и для координат, и для времени, в точности такие же, как и Эйнштейн, Паули, Левич, и Берклеевский курс физики, где используются другие методы вывода. И никаких трудностей, противоречий и нестыковок не возникает, результаты – в точности одинаковы, независимо от метода.
Теперь насчет «парадокса» с распиленной линейкой. Это – типичнейший пример «парадокса», вызванного неправильным пониманием, или непониманием теории относительности. Я уже неоднократно писал об этом, но вы, Людмила Михайловна, либо просто не читаете, либо не понимаете написанное. Кстати, В.С. Лебедев понял влет, сразу. Так вот, еще раз рассказываю.
Кажущиеся противоречащими здравому смыслу лоренцевские сокращения не являются реальными сокращениями. Это совершенно очевидно, так как в собственной системе отсчета никаких сокращений, типа от влияния эфирного ветра, как думал Лоренц, нет. Нет реальных сил, взаимодействий, которые вызвали бы такие сокращения. Измеряемые сокращения, зависящие от скорости, есть результаты измерений размеров (включая время) объекта в одной системе отсчета наблюдателем, находящимся в другой систем отсчета. При этом 4-мерный интервал, или его части: длины и промежутки времени, оказываются повернутыми по отношению к наблюдателю на угол, зависящий от скорости.
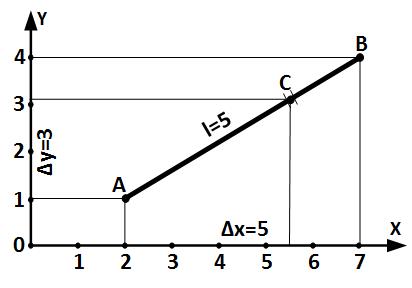
Рис. 1. Проекции отрезка.
Размеры этих проекций, а не реальные сокращения, и определяются преобразованиями Лоренца. На рис. 1 показан отрезок AB, длины его проекций на оси OX и OY очевидным образом зависят от ориентации отрезка в системе координат. Поверните его – и они изменятся. Если есть разрыв в точке C, то понятно, что ни при каких поворотах части AC и CB не будут разъезжаться друг от друга.
То же относится и к вашей разрезанной линейке. Если нет таких сил, которые заставят ее части разъединяться, то они и не будут этого делать.
Вывод:
«Вопиющих парадоксов» не отмечается. Вопиют в основном те, кто не знает и/или не понимает теорию относительности.
Вступите в группу, и вы сможете просматривать изображения в полном размере

Это интересно
0
|
|||

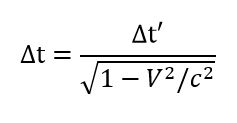


Последние откомментированные темы:
-
Ответы на детские вопросы про "Лунную Афёру"
(1)
kauperwud
,
28.02.2022
-
Космический корабль в несколько километров: все, что известно о новом проекте Китая
(2)
андрей1
,
27.02.2022
-
ЗАГАДКИ "ПАРАДОКСА ФЕРМИ" БОЛЬШЕ НЕТ?
(3)
donskarloss@gmail.com
,
27.02.2022
-
Марсианские реки
(1)
donskarloss@gmail.com
,
27.02.2022
-
Семь спорных причин считать, что на Земле существовали цивилизации до людей
(1)
donskarloss@gmail.com
,
24.02.2022
20250307054618