Не буду оспаривать принципиально те предположения, которые вы высказали в своей статье, хотя это и не означает, что я со всем эти согласен.
Однако при оценке влияния эффекта запаздывающего потенциала допущены принципиальные ошибки. Из-за полученных совершенно неправильных результатов делается глобальный вывод о дальнодействии вместо близкодействия для гравитационного взаимодействия.
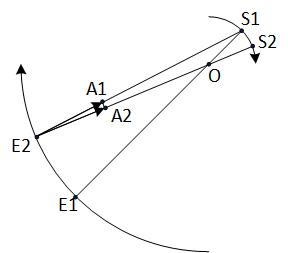
Итак, рассмотрим систему Земля – Солнце. Как справедливо отмечено в вашей статье, система вращается вокруг некоторого центра масс, обозначенного на рис.1 буквой О.
Рис.1
Пусть время τ есть время, за которое гравитационный сигнал от Солнца достигает Земли. За это время Солнце в данной системе центра масс проходит по своей орбите путь от точки S1 до точки S2, а Земля – от точки E1 до E2. В точке E2 до Земли доходит гравитационный сигнал от Солнца, когда оно находилось в точке S1. Из-за такого запоздания возникает тангенциальная составляющая силы тяготения, равная разности векторов силы притяжения A1 и A2. Для определения этой разности найдем угол α между этими векторами. Из-за малости этого угла с высокой степенью точности считаем, что sinα ≈ tgα ≈ α, а длина дуги между точками S1 и S2 равна длине отрезка прямой a = S1 S2, соединяющей эти точки.
Пусть также ω – угловая скорость вращения Земли вокруг Солнца, M и m – массы солнца и Земли, L – длина отрезка OE1, расстояние от Земли до Солнца, l – радиус орбиты Солнца в системе центра масс, длина отрезка OS1.
Тогда по определению: a = ωτl
Величину l определим из закона сохранения момента импульса. Из соотношения Ml = mL:
l = L / (M/m)
Тогда a = ωτL / (M/m). Следовательно, угол α в соответствии со сделанными допущениями равен
α = a / (L + l) = a / (L + L/(M+m)) ≈ a/L = ωτ / (M/m).
Или, если выразить τ через скорость распространения взаимодействия τ = L/c:
α = ωL / (c(M/m))
Величина искомой тангенциальной составляющей по модулю ΔA определится через этот угол как |A1|*α, а относительное ее значение по отношению к радиальной составляющей ΔA = |A1|*α / |A1| = α
Таким образом,
ΔA = α = ωτ / (M/m) = ωL / (c(M/m)) = (ωL/c) / (M/m)
Подставляем значения для Земли:
ω ≈ 2.0E-7 1/сек
L = 149.6 млн км ≈ 1.50E11
c = 299792458 м/сек ≈ 3.00E8 м/сек
ωL/c ≈ 9.96E-5
M/m = 332940 ≈ 3.33E5
откуда получаем:
ΔA ≈ 3.00E-10
Как видим, тангенциальная составляющая порядка 3E-10, что более чем на 6 порядков меньше, чем приводила в своей статье Л.М. Топтунова, которая совершенно неправильно рассчитывает силу.
Может показаться, что Земля имеет достаточно малую массу, поэтому так невелико значение ΔA. Вычислим это значение для Юпитера, самой большой планеты Солнечной системы.
Для Юпитера:
ω ≈ 1.68E-8 1/сек
L = 778 млн км
c = 299792458 м/сек ≈ 3.00E8 м/сек
ωL/c ≈ 4.36E-8
M/m = 1000
откуда получаем
ΔA ≈ 4.36E-11
– еще меньшее значение.
Таким образом, принципу близкодействия ничего не угрожает, и расчет влияния запаздывающих потенциалов, если оно вообще существует, не может привести к революции в физике.
К сказанному следует добавить еще некоторые замечания.
Во-первых. Понятное дело, что я не пытался решать задачу движения многих тел. Однако, по все видимости, учет движения всех планет Солнечной системы должен привести к некоторой компенсации положения Солнца относительно центра масс и дополнительно ослабить влияние запаздывающего потенциала, если оно вообще есть.
Во-вторых. Из приведенного рисунка видно, что если принять во внимание незначительное отклонение положения Солнца от центра масс, то положение точек S1 и S2 будет практически совпадать с точкой O. Следовательно, эффект аберрации, по крайней мере, на Земле, будет крайне незначительным. Поэтому и не стоит на него ссылаться.
Вступите в группу, и вы сможете просматривать изображения в полном размере

Это интересно
0
|
|||



Последние откомментированные темы:
-
Ответы на детские вопросы про "Лунную Афёру"
(1)
kauperwud
,
28.02.2022
-
Космический корабль в несколько километров: все, что известно о новом проекте Китая
(2)
андрей1
,
27.02.2022
-
ЗАГАДКИ "ПАРАДОКСА ФЕРМИ" БОЛЬШЕ НЕТ?
(3)
donskarloss@gmail.com
,
27.02.2022
-
Марсианские реки
(1)
donskarloss@gmail.com
,
27.02.2022
-
Семь спорных причин считать, что на Земле существовали цивилизации до людей
(1)
donskarloss@gmail.com
,
24.02.2022
20250125055440